pacman::p_load(sf, spdep, tmap, tidyverse)Hands-on Exercise 2B
9 Global and Local Measures of Spatial Autocorrelation
Note: This Hands-on Exercise 2B combines both 9 Global Measures of Spatial Autocorrelation and 10 Local Measures of Spatial Autocorrelation on r4gdsa.netlify.app since there are some overlaps in Sections 9.1 to 9.5.
9.1 Overview
In this page, I show how I had completed the Hands-on Exercise 2B, on computing Global and Local Measures of Spatial Autocorrelation (GLSA) using the spdep package.
The objectives are:
Import geospatial data using appropriate function(s) of sf package;
Import csv file using appropriate function of readr package;
Perform relational join using appropriate join function of dplyr package;
Compute Global Spatial Autocorrelation (GSA) statistics using appropriate functions of spdep package, including:
Plot Moran scatterplot,
Compute and plot spatial correlogram.
Compute Local Indicator of Spatial Association (LISA) statistics for detecting clusters and outliers using appropriate functions spdep package;
Compute Getis-Ord’s Gi statistics for detecting hot spot or/and cold spot area using appropriate functions of spdep package; and
Visualise the analysis output using tmap package.
9.2 Getting Started
9.2.1 The Analytical Question
In spatial policy, one of the main development objective of the local government and planners is to ensure equal distribution of development in the province.
Hence, the appropriate spatial statistical methods are applied to study:
Is development evenly distributed geographically?
If no, is there sign of spatial clustering? If yes, where are these clusters?
For this hands-on exercise, the GDP per capita (as a development indicator) of Hunan province in China is studied.
9.2.2 The Study Area and Data
The following data sets are used in this hands-on exercise:
Hunan’s County Boundary Layer. This is a geospatial data set in ESRI shapefile format.
Hunan’s Local Development Indicators 2012. This csv file contains data on selected Hunan’s local development indicators in 2012.
The data sets are placed under two sub-folders:
geospatial (County Boundary Layer), and
aspatial (Local Development Indicators 2012).
These two sub-folders are within the data folder of my Hands-on_Ex2 folder.
9.2.3 Setting the Analytical Tools
The R packages used in this hands-on exercises are:
tmap for thematic mapping;
sf for importing, managing, and processing geospatial data;
tidyverse (i.e. readr, tidyr, dplyr) for performing data science tasks such as importing, tidying, and wrangling data; and
spdep for analysing spatial dependence and spatial relationships in data.
They are loaded into the R environment using the following code:
Student Note: This allows for loading of multiple packages in one line of code.
9.3 Importing Data
9.3.1 Importing shapefile
The st_read() (under sf package) is used to import the geospatial data set: hunan, a polygon feature layer in ESRI shapefile format.
Student Note: The geospatial objects are polygon features. There are a total of 88 features and 7 fields in hunan simple feature data frame. hunan is in wgs84 coordinate system.
hunan = st_read(dsn = "data/geospatial",
layer = "Hunan")Reading layer `Hunan' from data source
`C:\jmphosis\ISSS624\Hands-on_Ex\Hands-on_Ex2\data\geospatial'
using driver `ESRI Shapefile'
Simple feature collection with 88 features and 7 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS: WGS 849.3.2 Importing csv file
The read_csv() (under readr package) is used to import the aspatial data set: hunan_2012, a csv file.
Student Note: The hunan_2012 tibble data frame contains 88 rows and 29 columns. There are two columns with character data - County and City.
hunan2012 = read_csv("data/aspatial/Hunan_2012.csv")9.3.3 Performing Relational Join
The attribute table of the spatial polygons data frame, hunan, is updated using the attribute fields of the tibble data frame, hunan2012 using left_join() (under dplyr package).
Student Note: Without explicitly stating the “by” argument for left_join(), the two tables are joined by the ‘County’ columns.
hunan = left_join(hunan,hunan2012) %>%
select(1:4, 7, 15)
hunanSimple feature collection with 88 features and 6 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS: WGS 84
First 10 features:
NAME_2 ID_3 NAME_3 ENGTYPE_3 County GDPPC
1 Changde 21098 Anxiang County Anxiang 23667
2 Changde 21100 Hanshou County Hanshou 20981
3 Changde 21101 Jinshi County City Jinshi 34592
4 Changde 21102 Li County Li 24473
5 Changde 21103 Linli County Linli 25554
6 Changde 21104 Shimen County Shimen 27137
7 Changsha 21109 Liuyang County City Liuyang 63118
8 Changsha 21110 Ningxiang County Ningxiang 62202
9 Changsha 21111 Wangcheng County Wangcheng 70666
10 Chenzhou 21112 Anren County Anren 12761
geometry
1 POLYGON ((112.0625 29.75523...
2 POLYGON ((112.2288 29.11684...
3 POLYGON ((111.8927 29.6013,...
4 POLYGON ((111.3731 29.94649...
5 POLYGON ((111.6324 29.76288...
6 POLYGON ((110.8825 30.11675...
7 POLYGON ((113.9905 28.5682,...
8 POLYGON ((112.7181 28.38299...
9 POLYGON ((112.7914 28.52688...
10 POLYGON ((113.1757 26.82734...9.3.4 Visualising Regional Development Indicator
A basemap and a choropleth map are prepared usign qtm() (under tmap package) to visualise the 2012 Gross Domestic Product Per Capita (GDPPC).
Student Note: The two different styles used are “equal” and “quantile”. The equal style shows that high GDPPC (in absolute terms) is concentrated in a few counties in the northeast region. The quantile style shows that the top 50% of counties in terms of GDPPC are mainly on the east side of Hunan.
equal = tm_shape(hunan) +
tm_fill("GDPPC",
n = 5,
style = "equal") +
tm_borders(alpha = 0.5) +
tm_layout(main.title = "Equal interval classification")
quantile = tm_shape(hunan) +
tm_fill("GDPPC",
n = 5,
style = "quantile") +
tm_borders(alpha = 0.5) +
tm_layout(main.title = "Equal quantile classification")
tmap_arrange(equal,
quantile,
asp=1,
ncol=2)
9.4 Global Spatial Autocorrelation
The Global Spatial Autocorrelation (GSA) statistics are computed for the study area. Also, Spatial Complete Randomness (SCR) test for GSA is performed.
Student Note: The SCR test for GSR checks if the spatial distribution of GDPPC is entirely random and lacks any systematic spatial pattern. In other words, it assesses whether the observed spatial pattern of the GDPPC deviates significantly from what would be expected under spatial randomness.
9.4.1 Computing Contiguity Spatial Weights
Firstly, the spatial weights of the study area would need to be computed to define the neighbourhood relationships between the geographical units (i.e., county) in the study area.
The poly2nb() (under spdep package) is used to compute contiguity weight matrices for the study area. This function builds a neighbours list based on regions with contiguous boundaries.
The “queen” argument in the function is set to either TRUE (default) or FALSE. The TRUE option will return a list of first order neighbours using the Queen’s continguity criteria.
Student Note: According to Queen’s criteria, two regions are considered neighbours if they share any part of their boundary (even if it is a single point). This results in a more inclusive definition of neighbour relationships.
Student Note: The summary report below shows that there are 88 area units in
hunan. The most connected area unit (85) has 11 neighbours. The least connected area units (30 and 65) have only one neighbour each.
wm_q = poly2nb(hunan, queen = TRUE)
summary(wm_q)Neighbour list object:
Number of regions: 88
Number of nonzero links: 448
Percentage nonzero weights: 5.785124
Average number of links: 5.090909
Link number distribution:
1 2 3 4 5 6 7 8 9 11
2 2 12 16 24 14 11 4 2 1
2 least connected regions:
30 65 with 1 link
1 most connected region:
85 with 11 links9.4.2 Row-standardised Weights Matrix
Weights are assigned to each neighbouring polygon. The nb21listw() (under spdep package) is used to convert a neighborhood object, wm_q, to a listw object, rswm_q (style=“W”). This allows row-standardised distance weight matrices to be created, whereby each row sums to 1. The “style” argument influences the specific characteristics of the weights matrix.
For this hands-on exercise, the “style=”W”” is used, each neighboring polygon is assigned equal weight. This is accomplished by assigning the fraction 1/(#ofneighbors) to each neighboring county then summing the weighted income values. While this is the most intuitive way to summarise the neighbors’ values, its downside is that polygons along the edges of the study area will base their lagged values on fewer polygons thus potentially over- or under-estimating the true nature of the spatial autocorrelation in the data.
Student Note:
The “style” argument set to “W” specifies a binary spatial weight matrix, where the presence of a spatial relationship is indicated by 1, and absence by 0. All neighbouring units are considered equal in terms of their impact on the target unit, reflecting a uniform spatial relation
B is the basic binary coding.
C is globally standardised (sums over all links to n).
U is equal to C divided by the number of neighbours (sums over all links to unity).
S is the variance-stabilizing coding scheme proposed by Tiefelsdorf et al. 1999 (sums over all links to n).
The “zero.policy” argument returns lists of non-neighbours when set to TRUE. It means that weight vectors of zero length are inserted for regions without neighbour in the neighbours list. This in turn generates lag values of zero, equivalent to the sum of products of the zero row t(rep(0, length=length(neighbours))) %*% x, for arbitrary numerical vector x of length equal to the number of neighbours. The spatially lagged value of x for the zero-neighbour region will then be zero.
- This ensures that even regions without neighbors are included in the spatial weights matrix, and their spatial lag values are explicitly set to zero. This can be useful in certain analytical contexts where the treatment of regions without neighbours is important for the analysis.
rswm_q = nb2listw(wm_q,
style="W",
zero.policy = TRUE)
rswm_qCharacteristics of weights list object:
Neighbour list object:
Number of regions: 88
Number of nonzero links: 448
Percentage nonzero weights: 5.785124
Average number of links: 5.090909
Weights style: W
Weights constants summary:
n nn S0 S1 S2
W 88 7744 88 37.86334 365.91479.4.3 Global Spatial Autocorrelation: Moran’s I
Moran’s I statistics testing is performed using moran.test() (under spdep package) to study the GSA.
Question: What statistical conclusion can be drawn from the output below?
Answer:
The Moran’s I statistic of 0.300749970 suggests a positive spatial autocorrelation in the GDPPC variable.
The p-value of 1.095e-06 is very small, indicating a strong evidence to reject the null hypothesis of spatial randomness and support the alternative hypothesis.
The alternative hypothesis is that there is a significant positive autocorrelation in the GDPPC, i.e., neighbouring regions tend to have similar GDPPC values (cluster together).
moran.test(hunan$GDPPC,
listw = rswm_q,
zero.policy = TRUE,
na.action=na.omit)
Moran I test under randomisation
data: hunan$GDPPC
weights: rswm_q
Moran I statistic standard deviate = 4.7351, p-value = 1.095e-06
alternative hypothesis: greater
sample estimates:
Moran I statistic Expectation Variance
0.300749970 -0.011494253 0.004348351 9.4.3.1 Computing and Visualising Monte Carlo’s Moran’s I
A permutation test (999 simulations using Monte Carlo) for Moran’s I statistic is performed using moran.mc() (under spdep package).
Student Note:
The set.seed() is used to ensure reproducibility.
The “na.action = na.omit” argument specifies the action to be taken if there are missing values. In this case, any observations with missing values are omitted from the analysis.
The “+ 1” is typically added to the number of simulations because the observed value is also included in the distribution of simulated values.
Question: What statistical conclusion can be drawn from the output below?
Answer:
The Moran’s I statistic of 0.30075 suggests a positive spatial autocorrelation in the GDPPC variable.
The p-value of 0.001 is less than the commonly used significance level of 0.05, indicating a strong evidence to reject the null hypothesis of spatial randomness and support the alternative hypothesis.
The alternative hypothesis is that there is a significant positive autocorrelation in the GDPPC, i.e., neighbouring regions tend to have similar GDPPC values (cluster together).
The rank of 1,000 of the observed Moran’s I statistic compared to the simulated values means that the observed spatial pattern is unlikely to have occurred by random chance.
set.seed(1234)
bperm_moran = moran.mc(hunan$GDPPC,
listw=rswm_q,
nsim=999,
zero.policy = TRUE,
na.action=na.omit)
bperm_moran
Monte-Carlo simulation of Moran I
data: hunan$GDPPC
weights: rswm_q
number of simulations + 1: 1000
statistic = 0.30075, observed rank = 1000, p-value = 0.001
alternative hypothesis: greaterThe simulated Moran’s I test statistics can be observed in further detail by plotting the distribution of the statistical values as a histogram. The hist() and abline() (under graphics package) are used.
Student Note: The distribution of simulated values show that more than half are negative values (i.e., negative correlation). It also shows that the observed Moran’s I statistic of 0.30075 would be considered an outlier, and unlikely to have occurred by chance.
mean(bperm_moran$res[1:999])[1] -0.01504572var(bperm_moran$res[1:999])[1] 0.004371574summary(bperm_moran$res[1:999]) Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.18339 -0.06168 -0.02125 -0.01505 0.02611 0.27593 hist(bperm_moran$res,
freq=TRUE,
breaks=20,
xlab="Simulated Moran's I")
abline(v=0,
col="red") 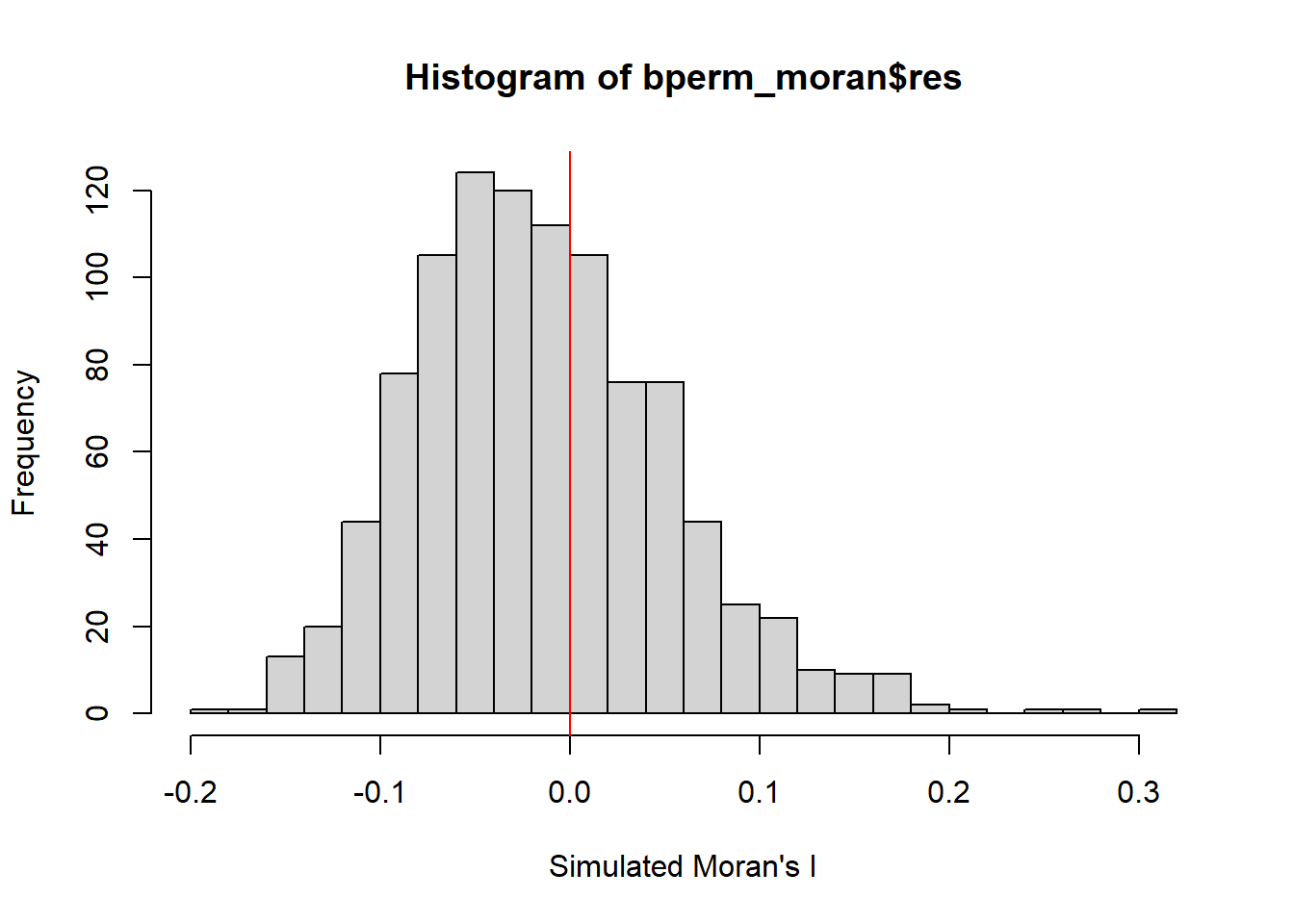
Alternatively, the graphs may be plotted using ggplot(), geom_histogram(), and geom_vline() (under ggplot2 package).
df = data.frame(Moran_I = bperm_moran$res[1:999])
ggplot(df, aes(x = Moran_I)) +
geom_histogram(binwidth = 0.02, fill = "light blue", color = "black", alpha = 0.7) +
labs(title = "Histogram of Simulated Moran's I",
x = "Simulated Moran's I",
y = "Frequency") +
theme_minimal() +
theme(panel.grid = element_blank()) +
geom_vline(xintercept = 0, color = "red", linetype = "dashed")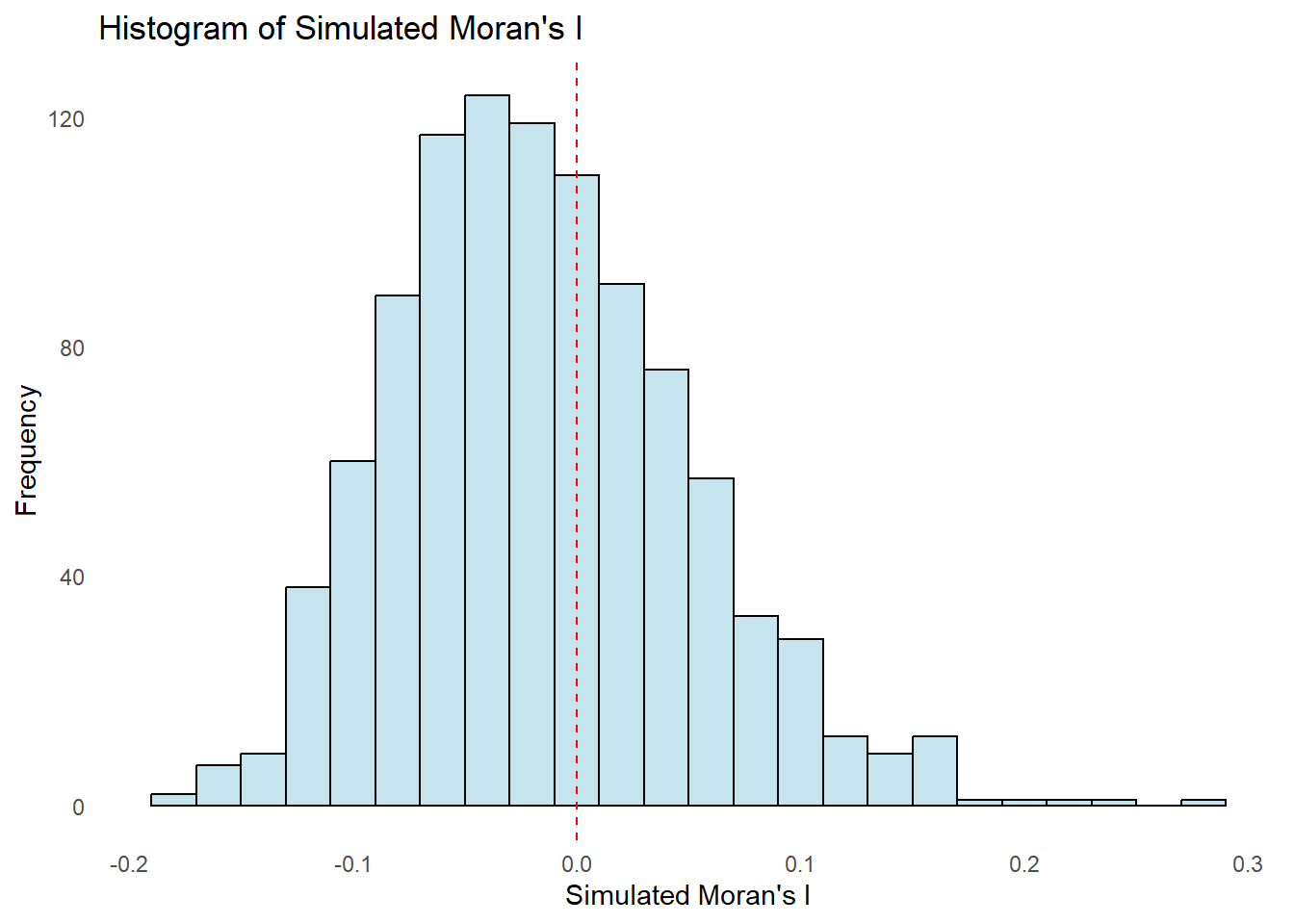
9.4.4 Global Spatial Autocorrelation: Geary’s C
Geary’s c statistics testing is performed using geary.test() (under spdep package) to study the GSA.
Question: What statistical conclusion can be drawn from the output below?
Answer:
The Geary’s c statistic of 0.6907223 suggests a positive spatial autocorrelation in the GDPPC variable, i.e., neighbouring regions tend to have similar GDPPC values.
The p-value of 0.0001526 is less than the commonly used significance level of 0.05, indicating a strong evidence to reject the null hypothesis of spatial randomness and support the alternative hypothesis.
The alternative hypothesis is that there is a significant positive autocorrelation in the GDPPC, i.e., neighbouring regions tend to have similar GDPPC values (cluster together).
geary.test(hunan$GDPPC, listw=rswm_q)
Geary C test under randomisation
data: hunan$GDPPC
weights: rswm_q
Geary C statistic standard deviate = 3.6108, p-value = 0.0001526
alternative hypothesis: Expectation greater than statistic
sample estimates:
Geary C statistic Expectation Variance
0.6907223 1.0000000 0.0073364 9.4.4.1 Computing and Visualising Monte Carlo Geary’s C
A permutation test (999 simulations using Monte Carlo) for Geary’s c statistic is performed using geary.mc() (under spdep package).
Student Note:
The set.seed() is used to ensure reproducibility.
The “+ 1” is typically added to the number of simulations because the observed value is also included in the distribution of simulated values.
Question: What statistical conclusion can be drawn from the output below?
Answer:
The Geary’s c statistic of 0.69072 suggests a positive spatial autocorrelation in the GDPPC variable.
The p-value of 0.001 is less than the commonly used significance level of 0.05, indicating a strong evidence to reject the null hypothesis of spatial randomness and support the alternative hypothesis.
The alternative hypothesis is that there is a significant positive autocorrelation in the GDPPC, i.e., neighbouring regions tend to have similar GDPPC values (cluster together).
The rank of 1 of the observed Geary’s c statistic compared to the simulated values means that the observed spatial pattern is unlikely to have occurred by random chance.
set.seed(1234)
bperm_geary=geary.mc(hunan$GDPPC,
listw=rswm_q,
nsim=999)
bperm_geary
Monte-Carlo simulation of Geary C
data: hunan$GDPPC
weights: rswm_q
number of simulations + 1: 1000
statistic = 0.69072, observed rank = 1, p-value = 0.001
alternative hypothesis: greaterThe simulated Geary’s c test statistics can be observed in further detail by plotting the distribution of the statistical values as a histogram. The hist() and abline() (under graphics package) are used.
Student Note: The distribution of simulated values show that more than half are abpve 1.0 (i.e., negative correlation). It also shows that the observed Geary’s c statistic of 69072 would be considered an outlier, and unlikely to have occurred by chance.
mean(bperm_geary$res[1:999])[1] 1.004402var(bperm_geary$res[1:999])[1] 0.007436493summary(bperm_geary$res[1:999]) Min. 1st Qu. Median Mean 3rd Qu. Max.
0.7142 0.9502 1.0052 1.0044 1.0595 1.2722 hist(bperm_geary$res, freq=TRUE, breaks=20, xlab="Simulated Geary c")
abline(v=1, col="red")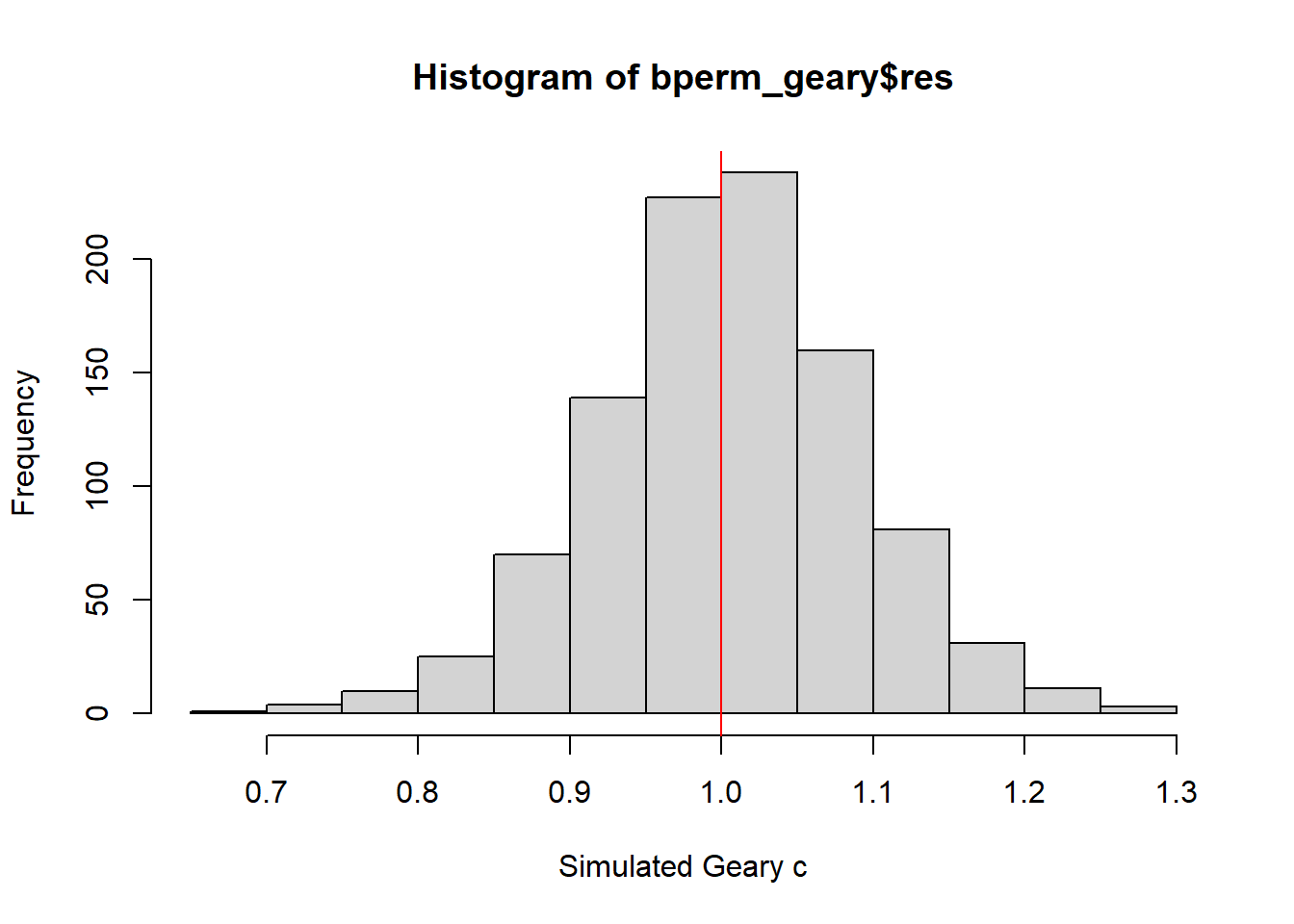
Alternatively, the graphs may be plotted using ggplot(), geom_histogram(), and geom_vline() (under ggplot2 package).
df = data.frame(Geary_C = bperm_geary$res[1:999])
ggplot(df, aes(x = Geary_C)) +
geom_histogram(binwidth = 0.02, fill = "light blue", color = "black", alpha = 0.7) +
labs(title = "Histogram of Simulated Geary's c",
x = "Simulated Geary's c",
y = "Frequency") +
theme_minimal() +
theme(panel.grid = element_blank()) +
geom_vline(xintercept = 1.0, color = "red", linetype = "dashed")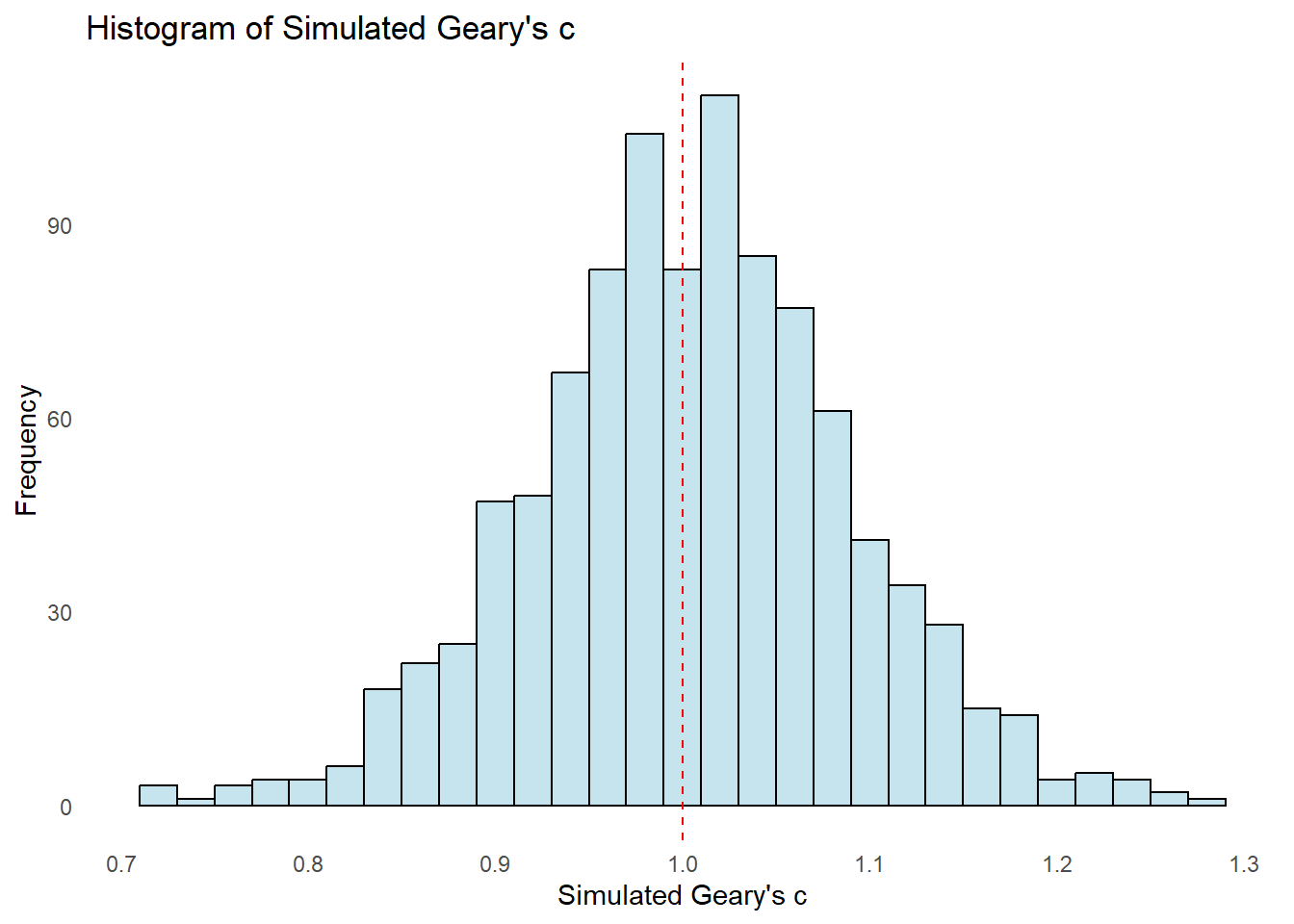
9.5 Spatial Correlogram
Spatial correlograms are great to examine patterns of spatial autocorrelation in the data or model residuals. They show how correlated pairs of spatial observations are when the distance (lag) between them is increased. They are plots of some index of autocorrelation (Moran’s I or Geary’s c) against distance.
Although correlograms are not as fundamental as variograms (a keystone concept of geostatistics), they are very useful as an exploratory and descriptive tool. For this purpose they actually provide richer information than variograms.
9.5.1 Computing and Visualising Moran’s I Correlogram
The sp.correlogram() (under spdep package) is used to compute a 6-lag spatial correlogram of the GDPPC variable. The GSA used is Moran’s I. The output is plotted using plot() (under graphics package).
Student Note: The “method=”I”” argument specifies that Moran’s I should be used as the measure of spatial autocorrelation.
Question: What statistical observation can be drawn from the plot below?
Answer:
Moran’s I estimates are positive at shorter distance lags (distance lags 1-4). The positive values suggest that neighbouring regions tend to have similar GDPPC values (cluster together).
Moran’s I estimates are negative at longer distance lags (distance lags 5-6). The negative values suggest that regions further away have dissimilar GDPPC values.
The p-values are generally very small (except for distance lag 4), indicating statistical significance, and high level of confidence to reject the null hypothesis of spatial randomness.
Overall, statistical significance observed for positive correlation at distance lags of 1-3, and negative correlation at distance lags of 5-6.
MI_corr = sp.correlogram(wm_q,
hunan$GDPPC,
order=6,
method="I",
style="W")
plot(MI_corr)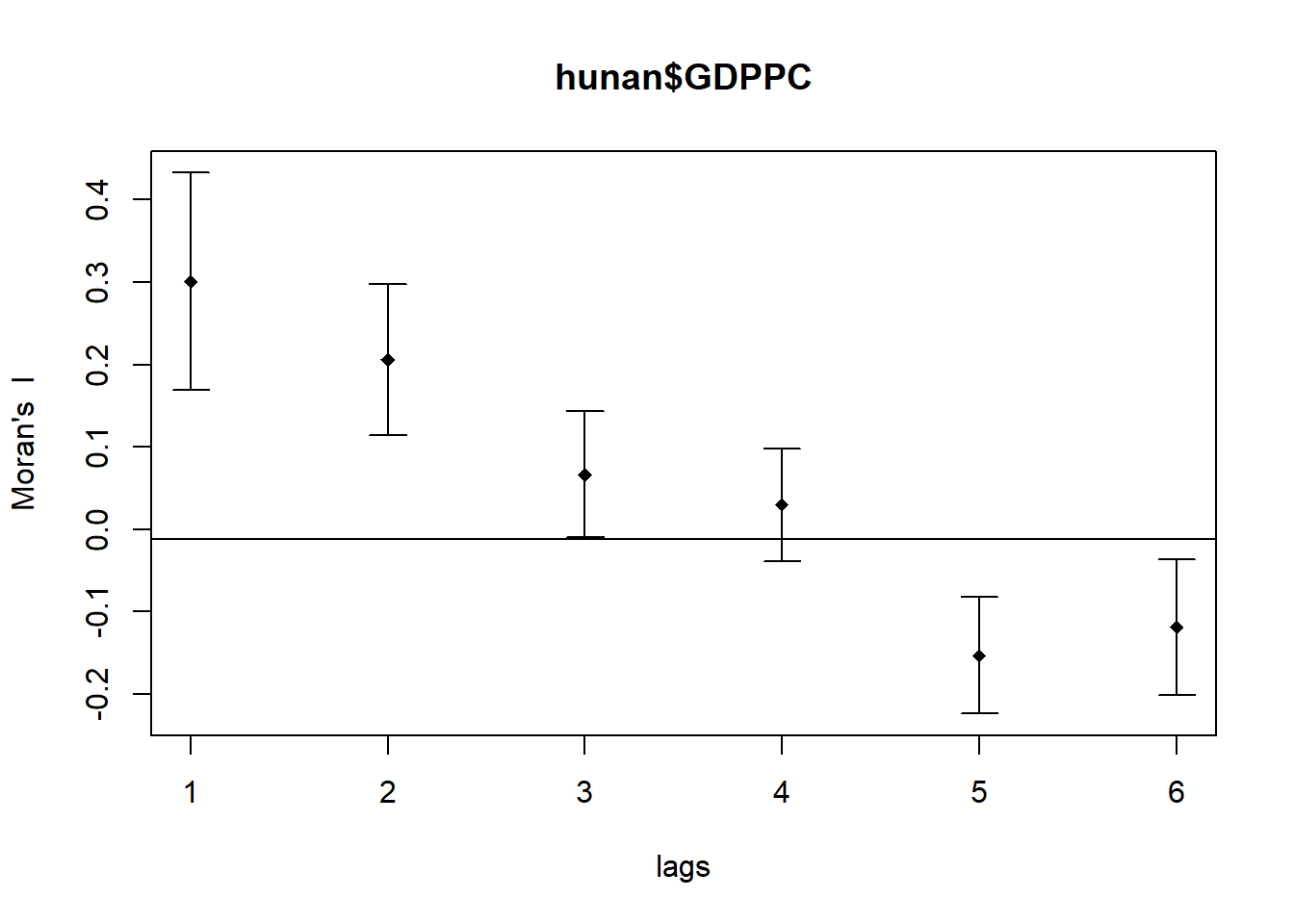
By plotting the output might not allow us to provide complete interpretation. This is because not all autocorrelation values are statistically significant. Hence, it is important to examine the full analysis report by printing out the analysis results.
print(MI_corr)Spatial correlogram for hunan$GDPPC
method: Moran's I
estimate expectation variance standard deviate Pr(I) two sided
1 (88) 0.3007500 -0.0114943 0.0043484 4.7351 2.189e-06 ***
2 (88) 0.2060084 -0.0114943 0.0020962 4.7505 2.029e-06 ***
3 (88) 0.0668273 -0.0114943 0.0014602 2.0496 0.040400 *
4 (88) 0.0299470 -0.0114943 0.0011717 1.2107 0.226015
5 (88) -0.1530471 -0.0114943 0.0012440 -4.0134 5.984e-05 ***
6 (88) -0.1187070 -0.0114943 0.0016791 -2.6164 0.008886 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 19.5.2 Computing and Visualising Geary’s C Correlogram
The sp.correlogram() (under spdep package) is used to compute a 6-lag spatial correlogram of the GDPPC variable. The GSA used is Geary’s c. The output is plotted using plot() (under graphics package).
Student Note: The “method=”C”” argument specifies that Geary’s c should be used as the measure of spatial autocorrelation.
Question: What statistical observation can be drawn from the plot below?
Answer:
Geary’s c estimates are below 1.0 at shorter distance lags (distance lags 1-3). These values suggest that neighbouring regions tend to have similar GDPPC values (cluster together).
Geary’s c estimates are above 1.0 at longer distance lags (distance lags 4-6). These values suggest that regions further away have dissimilar GDPPC values.
The p-values are small for distance lags 1, 2, and 5), indicating statistical significance, and high level of confidence to reject the null hypothesis of spatial randomness.
Overall, statistical significance observed for positive correlation at distance lags of 1-2, and negative correlation at distance lag of 5.
GC_corr = sp.correlogram(wm_q,
hunan$GDPPC,
order=6,
method="C",
style="W")
plot(GC_corr)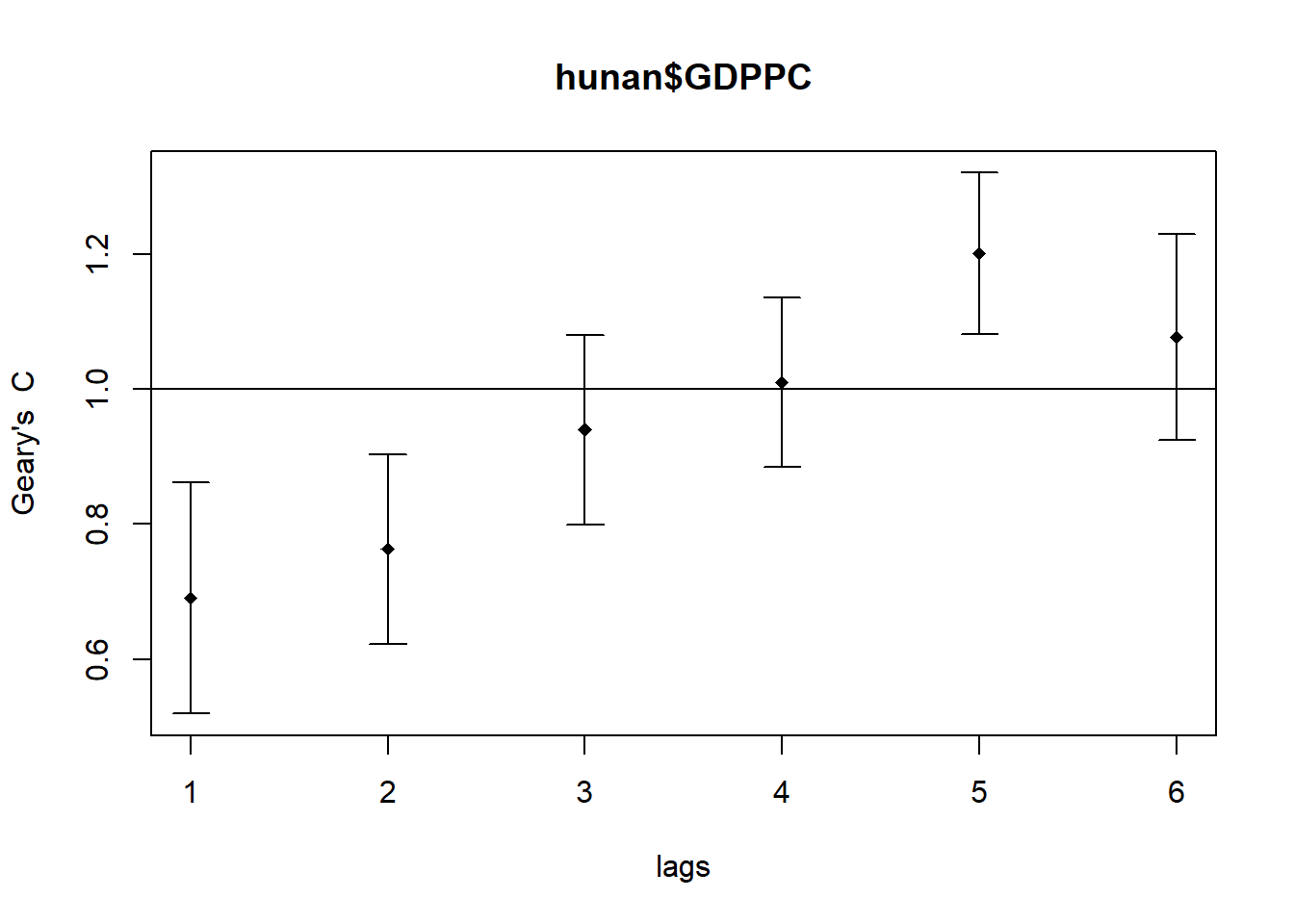
By plotting the output might not allow us to provide complete interpretation. This is because not all autocorrelation values are statistically significant. Hence, it is important to examine the full analysis report by printing out the analysis results.
print(GC_corr)Spatial correlogram for hunan$GDPPC
method: Geary's C
estimate expectation variance standard deviate Pr(I) two sided
1 (88) 0.6907223 1.0000000 0.0073364 -3.6108 0.0003052 ***
2 (88) 0.7630197 1.0000000 0.0049126 -3.3811 0.0007220 ***
3 (88) 0.9397299 1.0000000 0.0049005 -0.8610 0.3892612
4 (88) 1.0098462 1.0000000 0.0039631 0.1564 0.8757128
5 (88) 1.2008204 1.0000000 0.0035568 3.3673 0.0007592 ***
6 (88) 1.0773386 1.0000000 0.0058042 1.0151 0.3100407
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Note: The following sections follows 10 Local Measures of Spatial Autocorrelation (from Sections 10.6 onwards) on r4gdsa.netlify.app
10.6 Cluster and Outlier Analysis
Local Indicators of Spatial Association (LISA) are statistics that evaluate the existence of clusters in the spatial arrangement of a given variable.
The appropriate LISA, including local Moran’s I, are applied to detect cluster and/or outlier from the 2012 GDP per capita of the Hunan province in China.
10.6.1 Computing Local Moran’s I
The localmoran() (under spdep package) is used to compute the local Moran’s I. It computes Ii values, given a set of zi values and a listw object providing neighbour weighting information for the polygon associated with the zi values.
Ii: the local Moran’s I statistic.
E.Ii: the expectation of local Moran’s I statistic under the randomisation hypothesis.
Var.Ii: the variance of local Moran’s I statistic under the randomisation hypothesis.
Z.Ii: the standard deviate of local Moran’s I statistic.
Pr(): the p-value of local Moran’s I statistic.
Student Note:
Positive local Moran’s I values indicate a location surrounded by similar values (High-High or Low-Low).
Negative values indicate a location surrounded by dissimilar values (High-Low or Low-High).
Values near zero suggest no significant local spatial autocorrelation.
The local Moran’s I of the GDPPC at the county level is computed.
fips = order(hunan$County)
localMI = localmoran(hunan$GDPPC, rswm_q)
head(localMI) Ii E.Ii Var.Ii Z.Ii Pr(z != E(Ii))
1 -0.001468468 -2.815006e-05 4.723841e-04 -0.06626904 0.9471636
2 0.025878173 -6.061953e-04 1.016664e-02 0.26266425 0.7928094
3 -0.011987646 -5.366648e-03 1.133362e-01 -0.01966705 0.9843090
4 0.001022468 -2.404783e-07 5.105969e-06 0.45259801 0.6508382
5 0.014814881 -6.829362e-05 1.449949e-03 0.39085814 0.6959021
6 -0.038793829 -3.860263e-04 6.475559e-03 -0.47728835 0.6331568The contents of the local Moran’s I statistic matrix is derived using printCoefmat() (under stats package).
printCoefmat(data.frame(
localMI[fips,],
row.names=hunan$County[fips]),
check.names=FALSE) Ii E.Ii Var.Ii Z.Ii Pr.z....E.Ii..
Anhua -2.2493e-02 -5.0048e-03 5.8235e-02 -7.2467e-02 0.9422
Anren -3.9932e-01 -7.0111e-03 7.0348e-02 -1.4791e+00 0.1391
Anxiang -1.4685e-03 -2.8150e-05 4.7238e-04 -6.6269e-02 0.9472
Baojing 3.4737e-01 -5.0089e-03 8.3636e-02 1.2185e+00 0.2230
Chaling 2.0559e-02 -9.6812e-04 2.7711e-02 1.2932e-01 0.8971
Changning -2.9868e-05 -9.0010e-09 1.5105e-07 -7.6828e-02 0.9388
Changsha 4.9022e+00 -2.1348e-01 2.3194e+00 3.3590e+00 0.0008
Chengbu 7.3725e-01 -1.0534e-02 2.2132e-01 1.5895e+00 0.1119
Chenxi 1.4544e-01 -2.8156e-03 4.7116e-02 6.8299e-01 0.4946
Cili 7.3176e-02 -1.6747e-03 4.7902e-02 3.4200e-01 0.7324
Dao 2.1420e-01 -2.0824e-03 4.4123e-02 1.0297e+00 0.3032
Dongan 1.5210e-01 -6.3485e-04 1.3471e-02 1.3159e+00 0.1882
Dongkou 5.2918e-01 -6.4461e-03 1.0748e-01 1.6338e+00 0.1023
Fenghuang 1.8013e-01 -6.2832e-03 1.3257e-01 5.1198e-01 0.6087
Guidong -5.9160e-01 -1.3086e-02 3.7003e-01 -9.5104e-01 0.3416
Guiyang 1.8240e-01 -3.6908e-03 3.2610e-02 1.0305e+00 0.3028
Guzhang 2.8466e-01 -8.5054e-03 1.4152e-01 7.7931e-01 0.4358
Hanshou 2.5878e-02 -6.0620e-04 1.0167e-02 2.6266e-01 0.7928
Hengdong 9.9964e-03 -4.9063e-04 6.7742e-03 1.2742e-01 0.8986
Hengnan 2.8064e-02 -3.2160e-04 3.7597e-03 4.6294e-01 0.6434
Hengshan -5.8201e-03 -3.0437e-05 5.1076e-04 -2.5618e-01 0.7978
Hengyang 6.2997e-02 -1.3046e-03 2.1865e-02 4.3486e-01 0.6637
Hongjiang 1.8790e-01 -2.3019e-03 3.1725e-02 1.0678e+00 0.2856
Huarong -1.5389e-02 -1.8667e-03 8.1030e-02 -4.7503e-02 0.9621
Huayuan 8.3772e-02 -8.5569e-04 2.4495e-02 5.4072e-01 0.5887
Huitong 2.5997e-01 -5.2447e-03 1.1077e-01 7.9685e-01 0.4255
Jiahe -1.2431e-01 -3.0550e-03 5.1111e-02 -5.3633e-01 0.5917
Jianghua 2.8651e-01 -3.8280e-03 8.0968e-02 1.0204e+00 0.3076
Jiangyong 2.4337e-01 -2.7082e-03 1.1746e-01 7.1800e-01 0.4728
Jingzhou 1.8270e-01 -8.5106e-04 2.4363e-02 1.1759e+00 0.2396
Jinshi -1.1988e-02 -5.3666e-03 1.1334e-01 -1.9667e-02 0.9843
Jishou -2.8680e-01 -2.6305e-03 4.4028e-02 -1.3543e+00 0.1756
Lanshan 6.3334e-02 -9.6365e-04 2.0441e-02 4.4972e-01 0.6529
Leiyang 1.1581e-02 -1.4948e-04 2.5082e-03 2.3422e-01 0.8148
Lengshuijiang -1.7903e+00 -8.2129e-02 2.1598e+00 -1.1623e+00 0.2451
Li 1.0225e-03 -2.4048e-07 5.1060e-06 4.5260e-01 0.6508
Lianyuan -1.4672e-01 -1.8983e-03 1.9145e-02 -1.0467e+00 0.2952
Liling 1.3774e+00 -1.5097e-02 4.2601e-01 2.1335e+00 0.0329
Linli 1.4815e-02 -6.8294e-05 1.4499e-03 3.9086e-01 0.6959
Linwu -2.4621e-03 -9.0703e-06 1.9258e-04 -1.7676e-01 0.8597
Linxiang 6.5904e-02 -2.9028e-03 2.5470e-01 1.3634e-01 0.8916
Liuyang 3.3688e+00 -7.7502e-02 1.5180e+00 2.7972e+00 0.0052
Longhui 8.0801e-01 -1.1377e-02 1.5538e-01 2.0787e+00 0.0376
Longshan 7.5663e-01 -1.1100e-02 3.1449e-01 1.3690e+00 0.1710
Luxi 1.8177e-01 -2.4855e-03 3.4249e-02 9.9561e-01 0.3194
Mayang 2.1852e-01 -5.8773e-03 9.8049e-02 7.1663e-01 0.4736
Miluo 1.8704e+00 -1.6927e-02 2.7925e-01 3.5715e+00 0.0004
Nan -9.5789e-03 -4.9497e-04 6.8341e-03 -1.0988e-01 0.9125
Ningxiang 1.5607e+00 -7.3878e-02 8.0012e-01 1.8274e+00 0.0676
Ningyuan 2.0910e-01 -7.0884e-03 8.2306e-02 7.5356e-01 0.4511
Pingjiang -9.8964e-01 -2.6457e-03 5.6027e-02 -4.1698e+00 0.0000
Qidong 1.1806e-01 -2.1207e-03 2.4747e-02 7.6396e-01 0.4449
Qiyang 6.1966e-02 -7.3374e-04 8.5743e-03 6.7712e-01 0.4983
Rucheng -3.6992e-01 -8.8999e-03 2.5272e-01 -7.1814e-01 0.4727
Sangzhi 2.5053e-01 -4.9470e-03 6.8000e-02 9.7972e-01 0.3272
Shaodong -3.2659e-02 -3.6592e-05 5.0546e-04 -1.4510e+00 0.1468
Shaoshan 2.1223e+00 -5.0227e-02 1.3668e+00 1.8583e+00 0.0631
Shaoyang 5.9499e-01 -1.1253e-02 1.3012e-01 1.6807e+00 0.0928
Shimen -3.8794e-02 -3.8603e-04 6.4756e-03 -4.7729e-01 0.6332
Shuangfeng 9.2835e-03 -2.2867e-03 3.1516e-02 6.5174e-02 0.9480
Shuangpai 8.0591e-02 -3.1366e-04 8.9838e-03 8.5358e-01 0.3933
Suining 3.7585e-01 -3.5933e-03 4.1870e-02 1.8544e+00 0.0637
Taojiang -2.5394e-01 -1.2395e-03 1.4477e-02 -2.1002e+00 0.0357
Taoyuan 1.4729e-02 -1.2039e-04 8.5103e-04 5.0903e-01 0.6107
Tongdao 4.6482e-01 -6.9870e-03 1.9879e-01 1.0582e+00 0.2900
Wangcheng 4.4220e+00 -1.1067e-01 1.3596e+00 3.8873e+00 0.0001
Wugang 7.1003e-01 -7.8144e-03 1.0710e-01 2.1935e+00 0.0283
Xiangtan 2.4530e-01 -3.6457e-04 3.2319e-03 4.3213e+00 0.0000
Xiangxiang 2.6271e-01 -1.2703e-03 2.1290e-02 1.8092e+00 0.0704
Xiangyin 5.4525e-01 -4.7442e-03 7.9236e-02 1.9539e+00 0.0507
Xinhua 1.1810e-01 -6.2649e-03 8.6001e-02 4.2409e-01 0.6715
Xinhuang 1.5725e-01 -4.1820e-03 3.6648e-01 2.6667e-01 0.7897
Xinning 6.8928e-01 -9.6674e-03 2.0328e-01 1.5502e+00 0.1211
Xinshao 5.7578e-02 -8.5932e-03 1.1769e-01 1.9289e-01 0.8470
Xintian -7.4050e-03 -5.1493e-03 1.0877e-01 -6.8395e-03 0.9945
Xupu 3.2406e-01 -5.7468e-03 5.7735e-02 1.3726e+00 0.1699
Yanling -6.9021e-02 -5.9211e-04 9.9306e-03 -6.8667e-01 0.4923
Yizhang -2.6844e-01 -2.2463e-03 4.7588e-02 -1.2202e+00 0.2224
Yongshun 6.3064e-01 -1.1350e-02 1.8830e-01 1.4795e+00 0.1390
Yongxing 4.3411e-01 -9.0735e-03 1.5088e-01 1.1409e+00 0.2539
You 7.8750e-02 -7.2728e-03 1.2116e-01 2.4714e-01 0.8048
Yuanjiang 2.0004e-04 -1.7760e-04 2.9798e-03 6.9181e-03 0.9945
Yuanling 8.7298e-03 -2.2981e-06 2.3221e-05 1.8121e+00 0.0700
Yueyang 4.1189e-02 -1.9768e-04 2.3113e-03 8.6085e-01 0.3893
Zhijiang 1.0476e-01 -7.8123e-04 1.3100e-02 9.2214e-01 0.3565
Zhongfang -2.2685e-01 -2.1455e-03 3.5927e-02 -1.1855e+00 0.2358
Zhuzhou 3.2864e-01 -5.2432e-04 7.2391e-03 3.8688e+00 0.0001
Zixing -7.6849e-01 -8.8210e-02 9.4057e-01 -7.0144e-01 0.4830The local Moran’s I dataframe (i.e. localMI) is then appended onto hunan SpatialPolygonDataFrame. The output SpatialPolygonDataFrame is called hunan.localMI.
hunan.localMI = cbind(hunan,localMI) %>%
rename(Pr.Ii = Pr.z....E.Ii..)10.6.2 Mapping Local Moran’s I values and p-values
Using choropleth mapping functions of tmap package, the local Moran’s I values are plotted.
tm_shape(hunan.localMI) +
tm_fill(col = "Ii",
style = "pretty",
palette = "RdBu",
title = "local moran statistics") +
tm_borders(alpha = 0.5)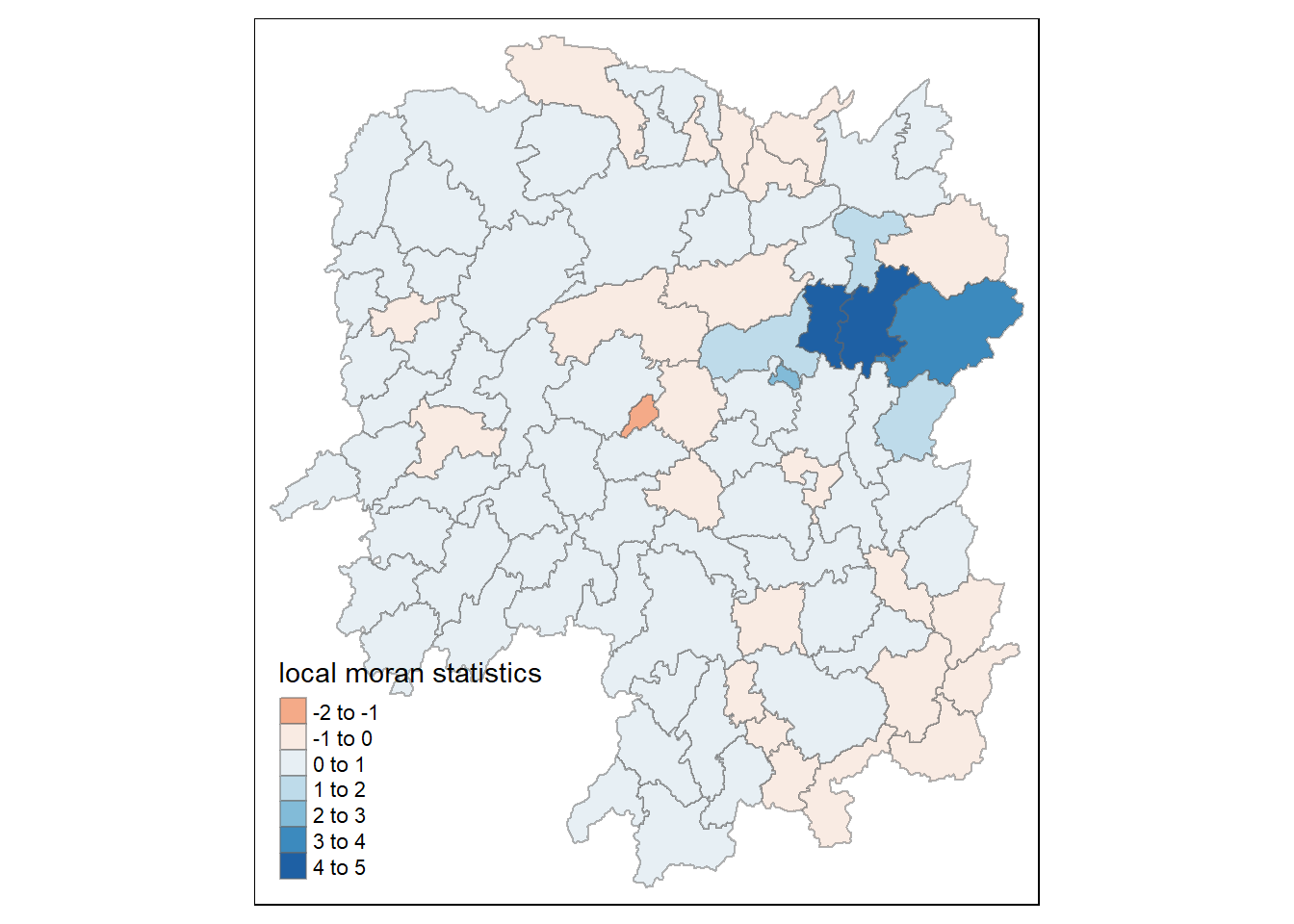
The choropleth shows evidence of both positive and negative Ii values. However, it is useful to consider the p-values for each of these values to see their statistical significance. A choropleth map of Moran’s I p-values using functions of tmap package is plotted below.
tm_shape(hunan.localMI) +
tm_fill(col = "Pr.Ii",
breaks=c(-Inf, 0.001, 0.01, 0.05, 0.1, Inf),
palette="-Blues",
title = "local Moran's I p-values") +
tm_borders(alpha = 0.5)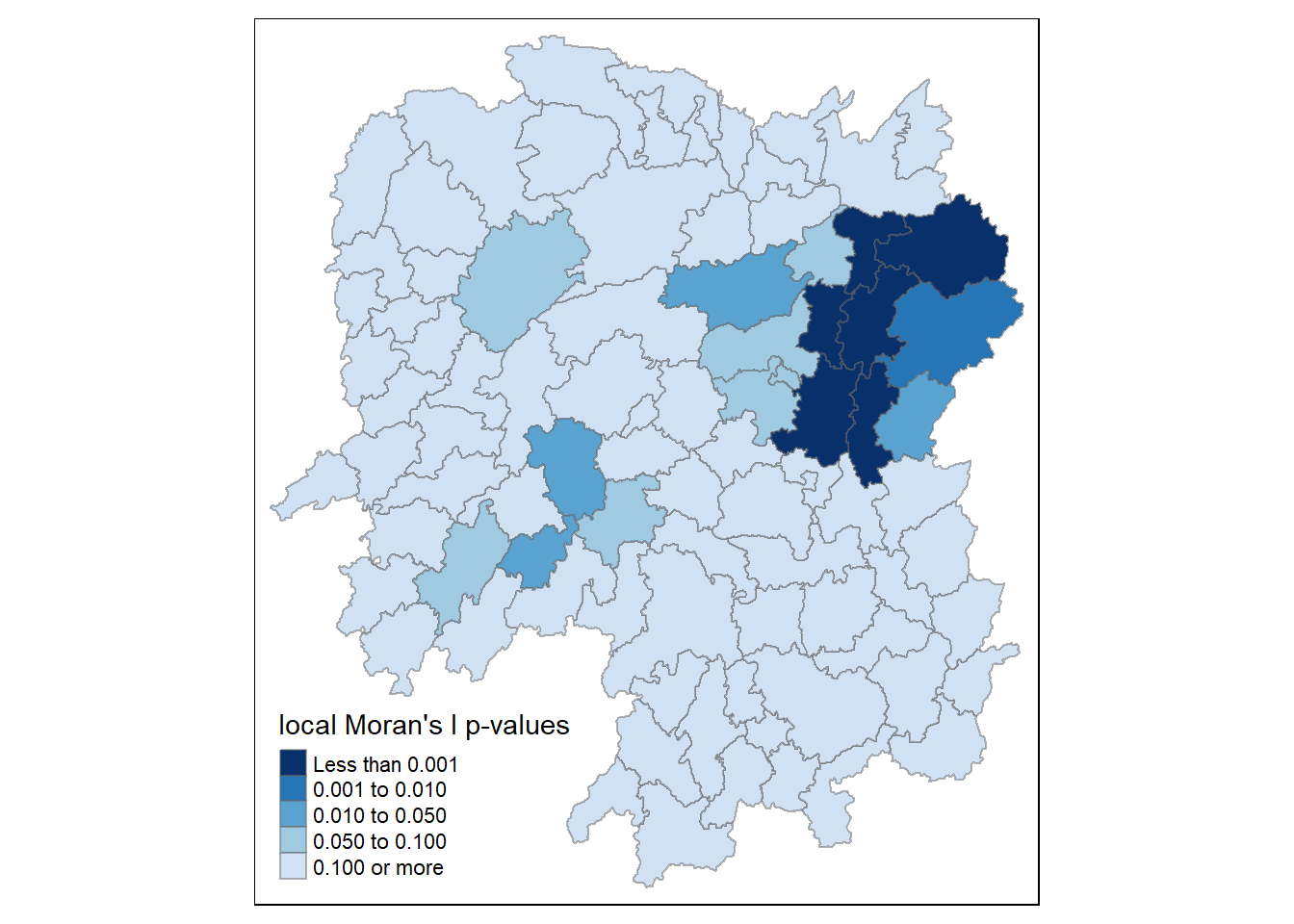
Putting the two plots side by side:
localMI.map = tm_shape(hunan.localMI) +
tm_fill(col = "Ii",
style = "pretty",
title = "local moran statistics") +
tm_borders(alpha = 0.5)
pvalue.map = tm_shape(hunan.localMI) +
tm_fill(col = "Pr.Ii",
breaks=c(-Inf, 0.001, 0.01, 0.05, 0.1, Inf),
palette="-Blues",
title = "local Moran's I p-values") +
tm_borders(alpha = 0.5)
tmap_arrange(localMI.map, pvalue.map, asp=1, ncol=2)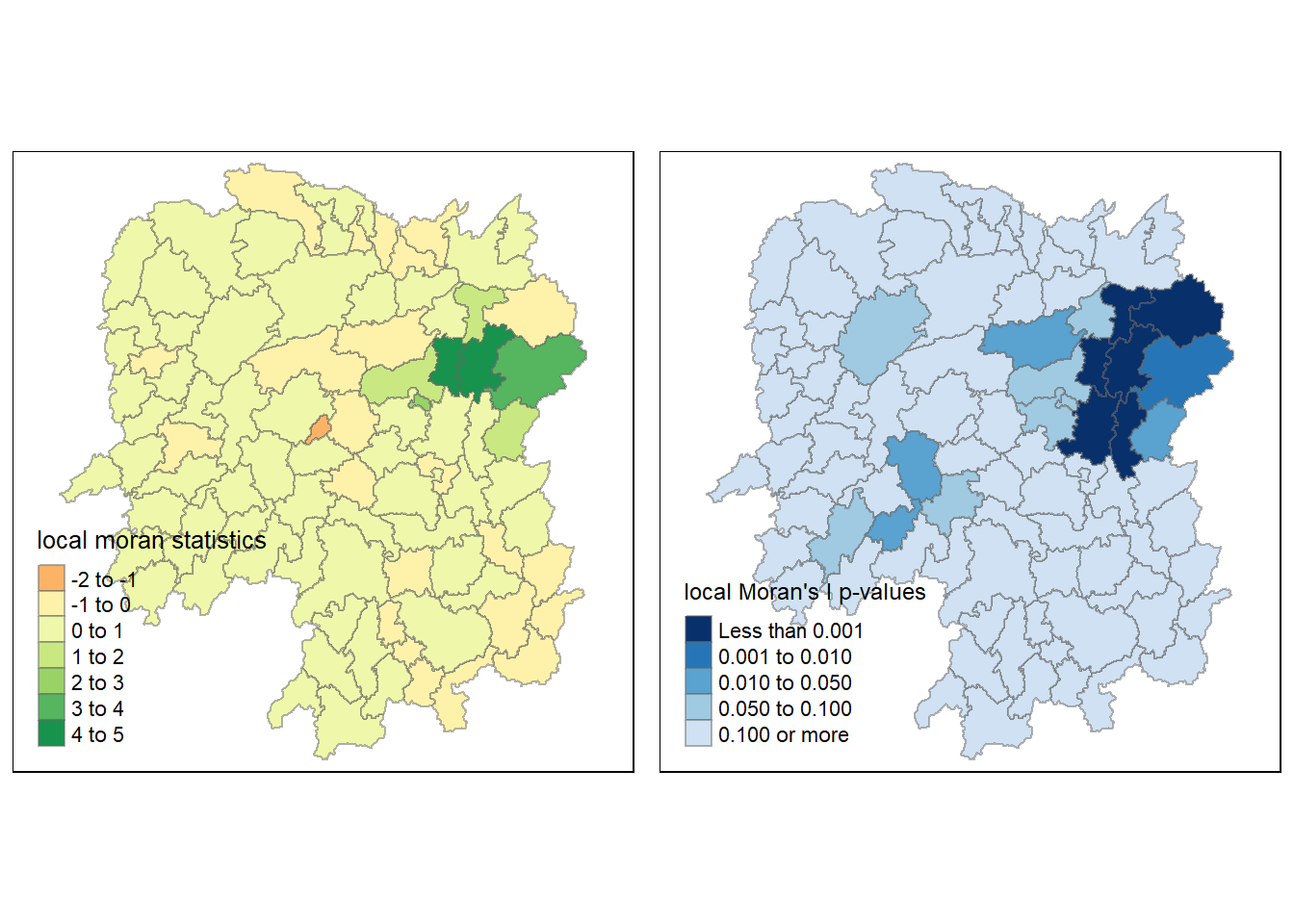
10.7 Creating a Local Indicators of Spatial Association (LISA) Cluster Map
The LISA Cluster Map shows the significant locations that are colour coded by the type of spatial autocorrelation.
Before generating the LISA cluster map, the Moran scatterplot is plotted.
10.7.1 Plotting Moran Scatterplot
The moran.plot() (under spdep package) is used to plot the Moran scatterplot, which is an illustration of the relationship between the values of the chosen attribute at each location and the average value of the same attribute at neighboring locations.
The plot is split in 4 quadrants. The top right corner belongs to areas that have high GDPPC and are surrounded by other areas that have the average level of GDPPC. These are the high-high locations.
nci = moran.plot(hunan$GDPPC, rswm_q,
labels=as.character(hunan$County),
xlab="GDPPC 2012",
ylab="Spatially Lag GDPPC 2012")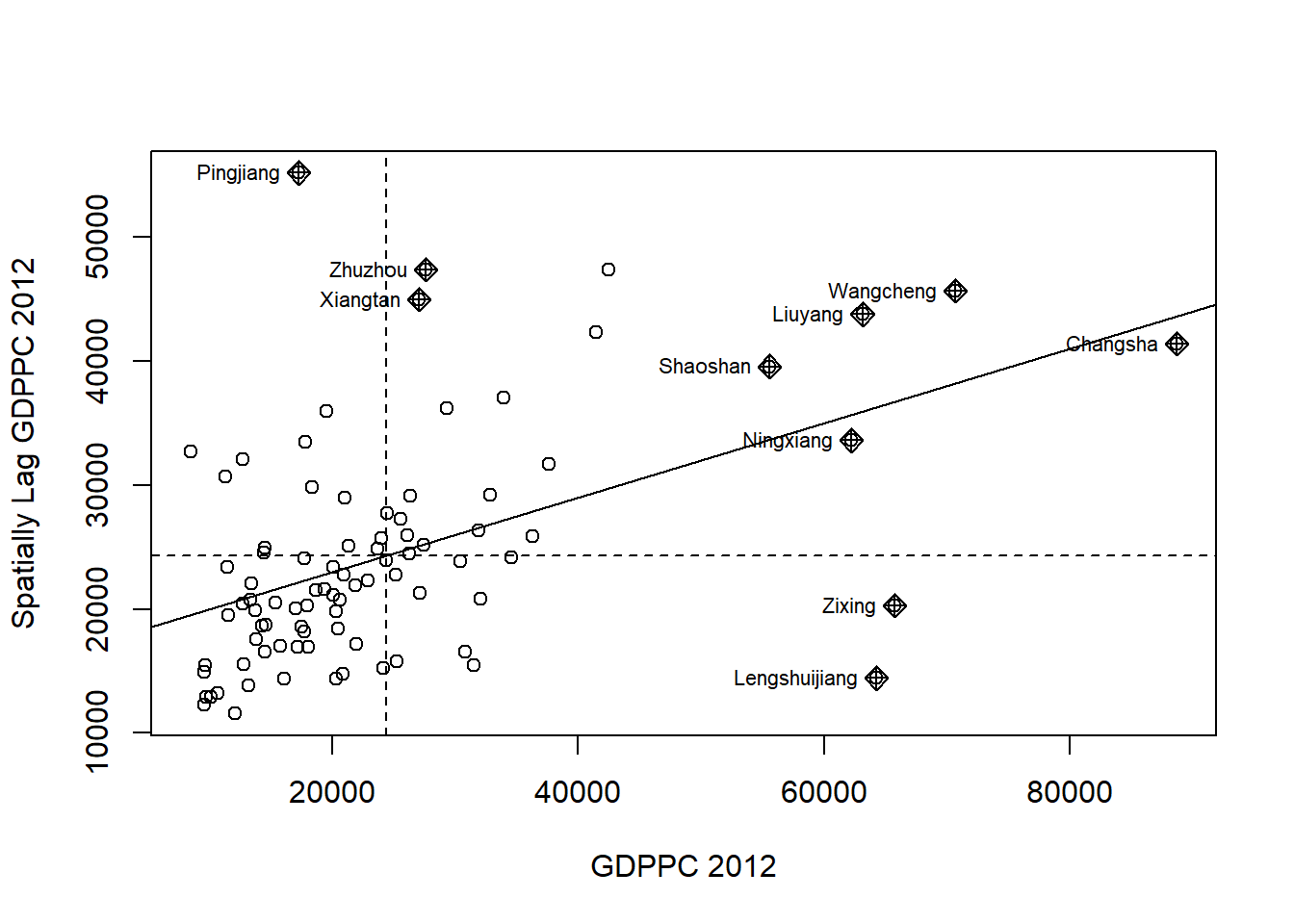
10.7.2 Plotting Moran Scatterplot with Standardised Variable
The scale() (from base package) is used to center and scale the variable. Centering is done by subtracting the mean (omitting NAs) of the corresponding columns, and scaling is done by dividing the (centered) variable by their standard deviations.
The as.vector() (under base package) is added to make sure that the data type derived is a vector that maps neatly into the dataframe.
hunan$Z.GDPPC = scale(hunan$GDPPC) %>%
as.vector
head(hunan)Simple feature collection with 6 features and 7 fields
Geometry type: POLYGON
Dimension: XY
Bounding box: xmin: 110.4922 ymin: 28.61762 xmax: 112.3013 ymax: 30.12812
Geodetic CRS: WGS 84
NAME_2 ID_3 NAME_3 ENGTYPE_3 County GDPPC
1 Changde 21098 Anxiang County Anxiang 23667
2 Changde 21100 Hanshou County Hanshou 20981
3 Changde 21101 Jinshi County City Jinshi 34592
4 Changde 21102 Li County Li 24473
5 Changde 21103 Linli County Linli 25554
6 Changde 21104 Shimen County Shimen 27137
geometry Z.GDPPC
1 POLYGON ((112.0625 29.75523... -0.049205949
2 POLYGON ((112.2288 29.11684... -0.228341158
3 POLYGON ((111.8927 29.6013,... 0.679406172
4 POLYGON ((111.3731 29.94649... 0.004547952
5 POLYGON ((111.6324 29.76288... 0.076642204
6 POLYGON ((110.8825 30.11675... 0.182215933The Moran scatterplot is then plotted again.
nci2 = moran.plot(hunan$Z.GDPPC, rswm_q,
labels=as.character(hunan$County),
xlab="z-GDPPC 2012",
ylab="Spatially Lag z-GDPPC 2012")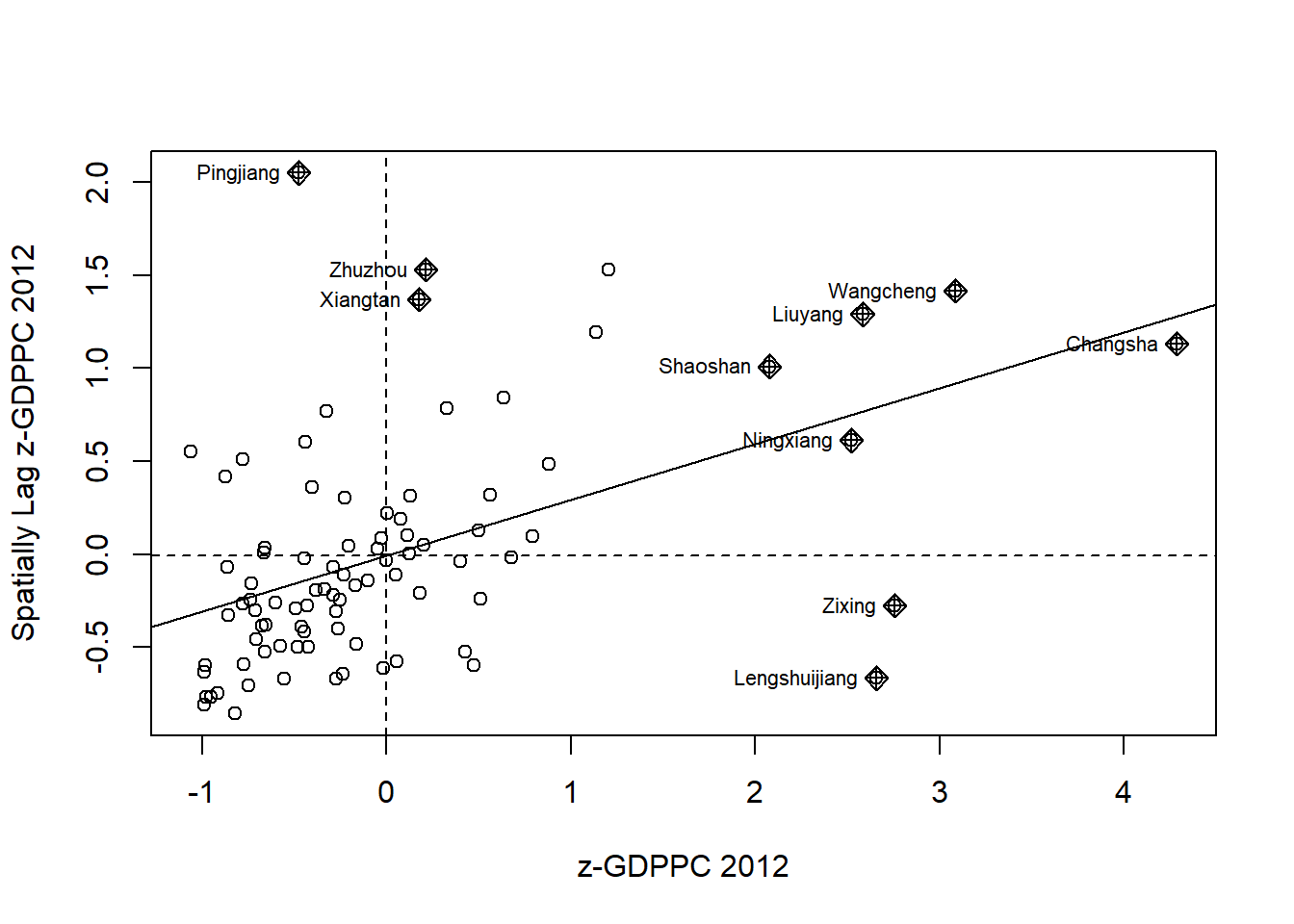
10.7.3 Preparing LISA Map Classes and Plotting LISA Map
To plot a LISA cluster map, the following steps are taken:
The spatially lagged variable of interest (GDPPC) is derived and centered around its mean.
The local Moran’s I is centered around the mean.
The statistical significance level for the local Moran’s I is set at 0.05.
The four quadrants are then defined.
Non-significant Moran’s I are then placed in the category 0.
quadrant = vector(mode="numeric",length=nrow(localMI))
hunan$lag_GDPPC = lag.listw(rswm_q, hunan$GDPPC)
DV = hunan$lag_GDPPC - mean(hunan$lag_GDPPC)
LM_I = localMI[,1]
signif = 0.05
quadrant[DV <0 & LM_I>0] = 1
quadrant[DV >0 & LM_I<0] = 2
quadrant[DV <0 & LM_I<0] = 3
quadrant[DV >0 & LM_I>0] = 4
quadrant[localMI[,5]>signif] = 0The LISA map is then plotted.
hunan.localMI$quadrant = quadrant
colors = c("#ffffff", "#2c7bb6", "#abd9e9", "#fdae61", "#d7191c")
clusters = c("insignificant", "low-low", "low-high", "high-low", "high-high")
tm_shape(hunan.localMI) +
tm_fill(col = "quadrant",
style = "cat",
palette = colors[c(sort(unique(quadrant)))+1],
labels = clusters[c(sort(unique(quadrant)))+1],
popup.vars = c("")) +
tm_view(set.zoom.limits = c(11,17)) +
tm_borders(alpha=0.5)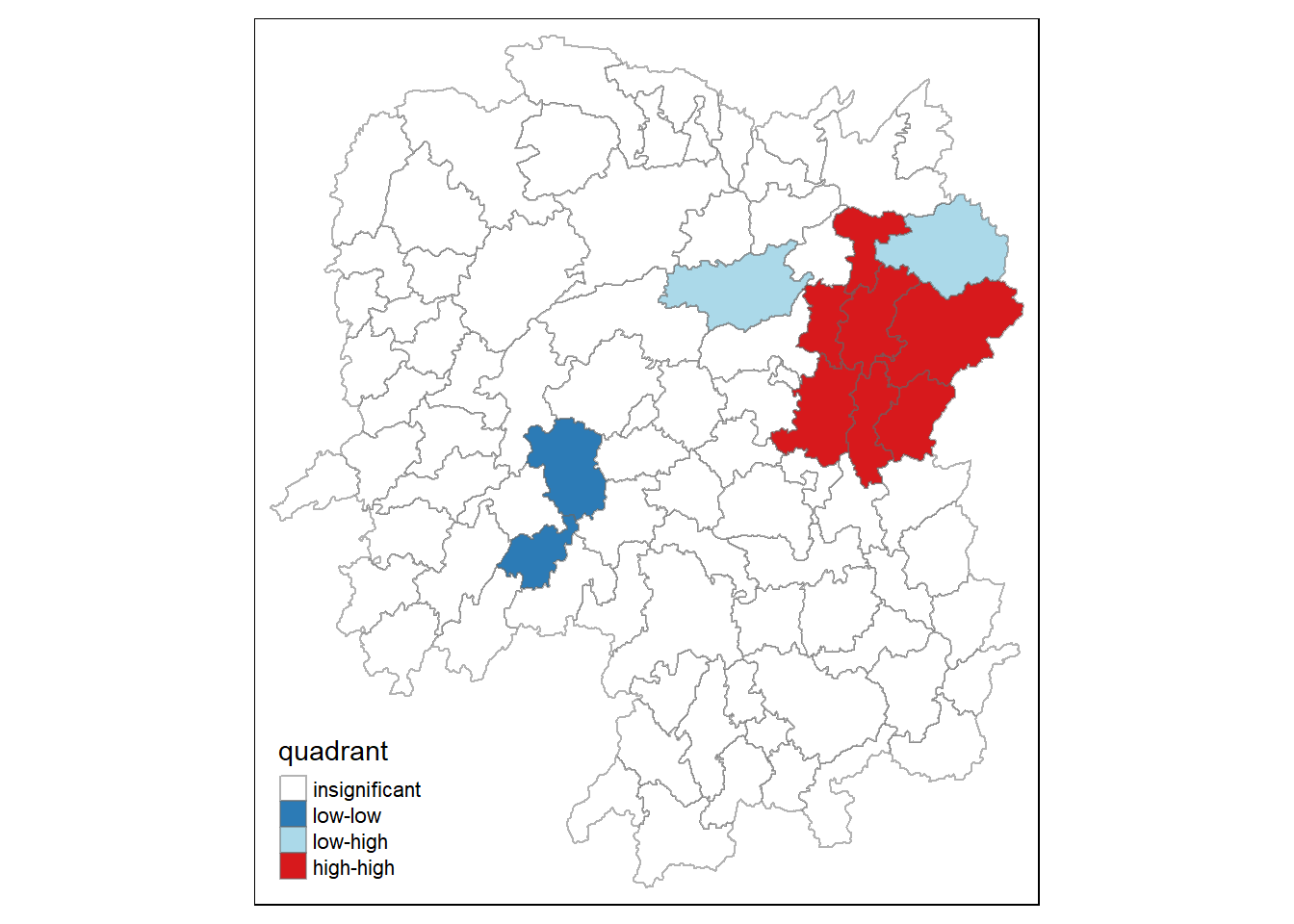
For effective interpretation, both the local Moran’s I values map and its corresponding p-values map are plotted side by side.
Question: What statistical observations can be drawn from the LISA map below?
Answer:
Most of the Moran’s I values are insignificant.
There are two low-low GDPPC counties in the central-west region. Based on the local Moran’s I p-values, they are statistically significant.
There are some high-high GDPPC counties in the northeast region. Based on the local Moran’s I p-values, they are statistically significant.
There are also two counties with low-high GDPPC in the northeast region. These two countries have low GDPPC even though they are surrounded by counties with high GDPPC. Based on the local Moran’s I p-values, they are statistically significant.
gdppc = qtm(hunan, "GDPPC")
hunan.localMI$quadrant = quadrant
colors <- c("#ffffff", "#2c7bb6", "#abd9e9", "#fdae61", "#d7191c")
clusters = c("insignificant", "low-low", "low-high", "high-low", "high-high")
LISAmap = tm_shape(hunan.localMI) +
tm_fill(col = "quadrant",
style = "cat",
palette = colors[c(sort(unique(quadrant)))+1],
labels = clusters[c(sort(unique(quadrant)))+1],
popup.vars = c("")) +
tm_view(set.zoom.limits = c(11,17)) +
tm_borders(alpha=0.5)
tmap_arrange(gdppc, LISAmap,
asp=1, ncol=2)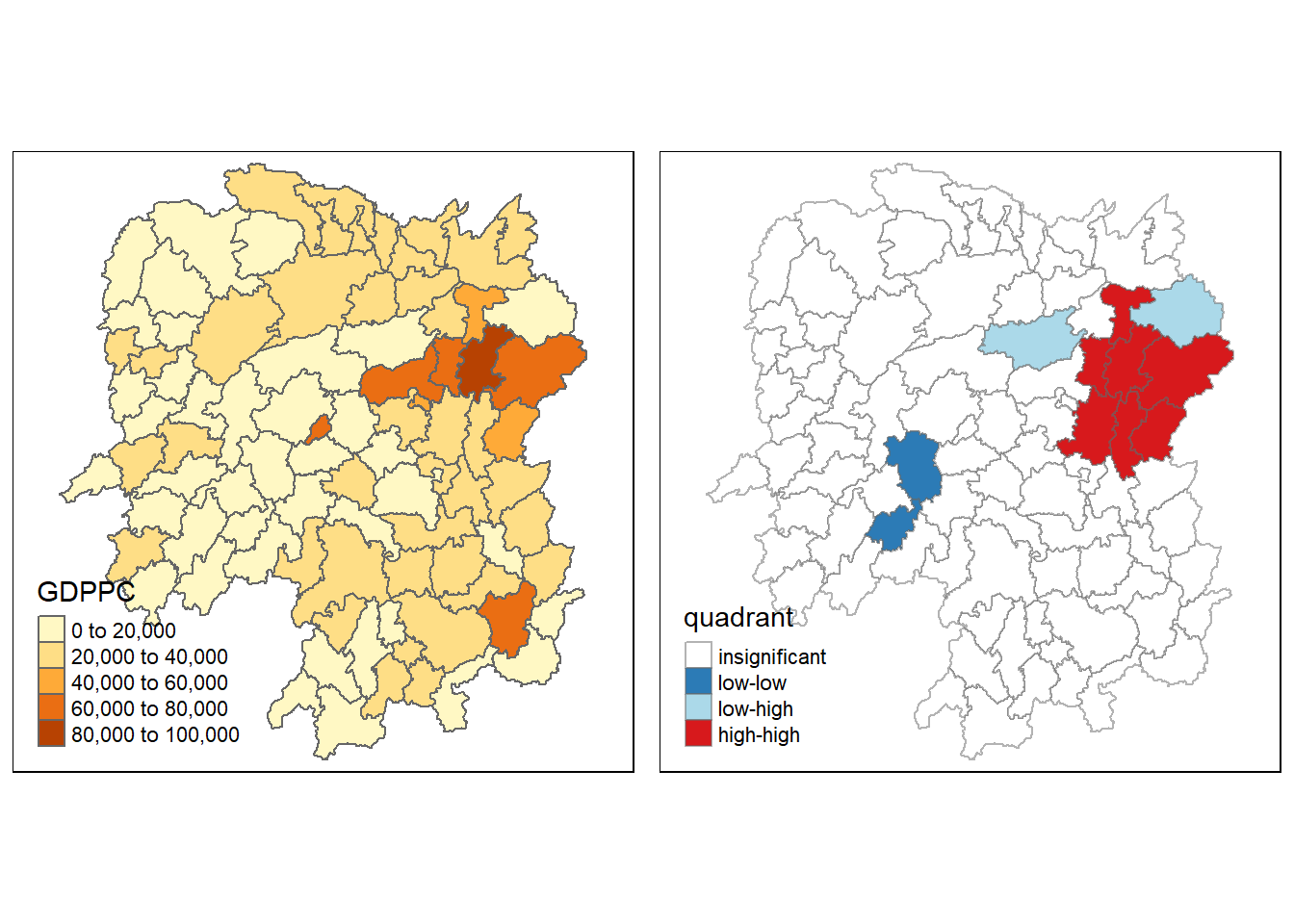
10.8 Hot Spot and Cold Spot Area Analysis
Beside detecting cluster and outliers, localised spatial statistics can be also used to detect hot spot and/or cold spot areas.
The term ‘hot spot’ has been used generically across disciplines to describe a region or value that is higher relative to its surroundings (Lepers et al 2005, Aben et al 2012, Isobe et al 2015).
10.8.1 Getis and Ord’s G-Statistics
An alternative spatial statistics to detect spatial anomalies is the Getis and Ord’s G-statistics (Getis and Ord, 1972; Ord and Getis, 1995). It looks at neighbours within a defined proximity to identify where either high or low values clutser spatially. Here, statistically significant hot spots are recognised as areas of high values where other areas within a neighbourhood range also share high values too.
The analysis consists of three steps:
Deriving spatial weight matrix;
Computing Gi statistics; and
Mapping Gi statistics.
10.8.2 Deriving Distance-based Weight Matrix
A new set of neighbours has to be defined. For Getis-Ord, neighbours are defined based on distance (as opposed to shared borders under spatial autocorrelation).
There are two types of distance-based proximity matrix:
Fixed distance weight matrix; and
Adaptive distance weight matrix.
10.8.2.1 Deriving the Centroid
Before making a connectivity graph, points are required to associate with each polygon
The mapping function, map_dbl() (under the purrr package) is utilised to apply a function, st_centroid() (under sf package), on each element of the geometry column, us.bound, returning a vector of a same length.
The longitude is then extracted by looking for the first value of each centroid, while the latitude is extracted by looking for the second value of each centroid. The cbind() is then used to put the two values together.
longitude = map_dbl(hunan$geometry, ~st_centroid(.x)[[1]])
latitude = map_dbl(hunan$geometry, ~st_centroid(.x)[[2]])
coords = cbind(longitude, latitude)10.8.2.2 Determining the Cut-Off Distance
The upper limit for the distance band is determined by using the following steps and functions under the spdep package:
Return a matrix with the indices of points belonging to the set of the k nearest neighbours (knn) of each other by using knearneigh().
Student Note: In the matrix, each row corresponds to a point, and the columns contain the indices of its knn.
Convert the knn object into a neighbours list of class nb with a list of integer vectors containing neighbour region number ids by using knn2nb().
Return the length of neighbour relationship edges by using nbdists(). This function returns in the units of the coordinates if the coordinates are projected, and in km otherwise.
Remove the list structure of the returned object by using unlist() (under base package).
The summary report below shows that the largest first nearest neighbour distance is 61.79 km (i.e., max value). Thus, this is used as the upper threshold as it ensures that all units will have at least one neighbour.
k1 = knn2nb(knearneigh(coords))
k1dists = unlist(nbdists(k1, coords, longlat = TRUE))
summary(k1dists) Min. 1st Qu. Median Mean 3rd Qu. Max.
24.79 32.57 38.01 39.07 44.52 61.79 10.8.2.3 Computing Fixed Distance Weight Matrix
The dnearneigh() (under spdep package) is used to compute the distance weight matrix.
Student Note: knearneigh() computes knn, while dnearneigh() computes distance-based neighbours.
wm_d62 = dnearneigh(coords, 0, 62, longlat = TRUE)
wm_d62Neighbour list object:
Number of regions: 88
Number of nonzero links: 324
Percentage nonzero weights: 4.183884
Average number of links: 3.681818 The nb2listw() (under spdep package) is then used to convert the nb object into spatial weights object, wm62_lw.
wm62_lw = nb2listw(wm_d62, style = 'B')
summary(wm62_lw)Characteristics of weights list object:
Neighbour list object:
Number of regions: 88
Number of nonzero links: 324
Percentage nonzero weights: 4.183884
Average number of links: 3.681818
Link number distribution:
1 2 3 4 5 6
6 15 14 26 20 7
6 least connected regions:
6 15 30 32 56 65 with 1 link
7 most connected regions:
21 28 35 45 50 52 82 with 6 links
Weights style: B
Weights constants summary:
n nn S0 S1 S2
B 88 7744 324 648 544010.8.3 Computing Adaptive Distance Weight Matrix
One of the characteristics of fixed distance weight matrix is that more densely settled areas (usually the urban areas) tend to have more neighbours and the less densely settled areas (usually the rural counties) tend to have lesser neighbours. Having many neighbours smoothes the neighbour relationship across more neighbours.
It is possible to control the numbers of neighbours directly using k-nearest neighbours, either accepting asymmetric neighbours or imposing symmetry as shown below.
knn = knn2nb(knearneigh(coords, k=8))
knnNeighbour list object:
Number of regions: 88
Number of nonzero links: 704
Percentage nonzero weights: 9.090909
Average number of links: 8
Non-symmetric neighbours listAgain, the nb2listw() (under spdep package) is used to convert the nb object into spatial weights object, knn_lw.
knn_lw = nb2listw(knn, style = 'B')
summary(knn_lw)Characteristics of weights list object:
Neighbour list object:
Number of regions: 88
Number of nonzero links: 704
Percentage nonzero weights: 9.090909
Average number of links: 8
Non-symmetric neighbours list
Link number distribution:
8
88
88 least connected regions:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 with 8 links
88 most connected regions:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 with 8 links
Weights style: B
Weights constants summary:
n nn S0 S1 S2
B 88 7744 704 1300 2301410.9 Computing Gi Statistics
10.9.1 Gi Statistics Using Fixed Distance and Mapping Gi Values with Fixed Distance Weights
The output of localG() (under spdep package) is a vector of G or Gstar values, with attributes “gstari” set to TRUE or FALSE, “call” set to the function call, and class “localG”.
The Gi statistics is represented as a Z-score. Greater values represent a greater intensity of clustering and the direction (positive or negative) indicates high or low clusters.
The Gi values for GDPPC 2012 is computed using fixed distance weights, wm62_lw.
fips = order(hunan$County)
gi.fixed = localG(hunan$GDPPC, wm62_lw)
gi.fixed [1] 0.436075843 -0.265505650 -0.073033665 0.413017033 0.273070579
[6] -0.377510776 2.863898821 2.794350420 5.216125401 0.228236603
[11] 0.951035346 -0.536334231 0.176761556 1.195564020 -0.033020610
[16] 1.378081093 -0.585756761 -0.419680565 0.258805141 0.012056111
[21] -0.145716531 -0.027158687 -0.318615290 -0.748946051 -0.961700582
[26] -0.796851342 -1.033949773 -0.460979158 -0.885240161 -0.266671512
[31] -0.886168613 -0.855476971 -0.922143185 -1.162328599 0.735582222
[36] -0.003358489 -0.967459309 -1.259299080 -1.452256513 -1.540671121
[41] -1.395011407 -1.681505286 -1.314110709 -0.767944457 -0.192889342
[46] 2.720804542 1.809191360 -1.218469473 -0.511984469 -0.834546363
[51] -0.908179070 -1.541081516 -1.192199867 -1.075080164 -1.631075961
[56] -0.743472246 0.418842387 0.832943753 -0.710289083 -0.449718820
[61] -0.493238743 -1.083386776 0.042979051 0.008596093 0.136337469
[66] 2.203411744 2.690329952 4.453703219 -0.340842743 -0.129318589
[71] 0.737806634 -1.246912658 0.666667559 1.088613505 -0.985792573
[76] 1.233609606 -0.487196415 1.626174042 -1.060416797 0.425361422
[81] -0.837897118 -0.314565243 0.371456331 4.424392623 -0.109566928
[86] 1.364597995 -1.029658605 -0.718000620
attr(,"internals")
Gi E(Gi) V(Gi) Z(Gi) Pr(z != E(Gi))
[1,] 0.064192949 0.05747126 2.375922e-04 0.436075843 6.627817e-01
[2,] 0.042300020 0.04597701 1.917951e-04 -0.265505650 7.906200e-01
[3,] 0.044961480 0.04597701 1.933486e-04 -0.073033665 9.417793e-01
[4,] 0.039475779 0.03448276 1.461473e-04 0.413017033 6.795941e-01
[5,] 0.049767939 0.04597701 1.927263e-04 0.273070579 7.847990e-01
[6,] 0.008825335 0.01149425 4.998177e-05 -0.377510776 7.057941e-01
[7,] 0.050807266 0.02298851 9.435398e-05 2.863898821 4.184617e-03
[8,] 0.083966739 0.04597701 1.848292e-04 2.794350420 5.200409e-03
[9,] 0.115751554 0.04597701 1.789361e-04 5.216125401 1.827045e-07
[10,] 0.049115587 0.04597701 1.891013e-04 0.228236603 8.194623e-01
[11,] 0.045819180 0.03448276 1.420884e-04 0.951035346 3.415864e-01
[12,] 0.049183846 0.05747126 2.387633e-04 -0.536334231 5.917276e-01
[13,] 0.048429181 0.04597701 1.924532e-04 0.176761556 8.596957e-01
[14,] 0.034733752 0.02298851 9.651140e-05 1.195564020 2.318667e-01
[15,] 0.011262043 0.01149425 4.945294e-05 -0.033020610 9.736582e-01
[16,] 0.065131196 0.04597701 1.931870e-04 1.378081093 1.681783e-01
[17,] 0.027587075 0.03448276 1.385862e-04 -0.585756761 5.580390e-01
[18,] 0.029409313 0.03448276 1.461397e-04 -0.419680565 6.747188e-01
[19,] 0.061466754 0.05747126 2.383385e-04 0.258805141 7.957856e-01
[20,] 0.057656917 0.05747126 2.371303e-04 0.012056111 9.903808e-01
[21,] 0.066518379 0.06896552 2.820326e-04 -0.145716531 8.841452e-01
[22,] 0.045599896 0.04597701 1.928108e-04 -0.027158687 9.783332e-01
[23,] 0.030646753 0.03448276 1.449523e-04 -0.318615290 7.500183e-01
[24,] 0.035635552 0.04597701 1.906613e-04 -0.748946051 4.538897e-01
[25,] 0.032606647 0.04597701 1.932888e-04 -0.961700582 3.362000e-01
[26,] 0.035001352 0.04597701 1.897172e-04 -0.796851342 4.255374e-01
[27,] 0.012746354 0.02298851 9.812587e-05 -1.033949773 3.011596e-01
[28,] 0.061287917 0.06896552 2.773884e-04 -0.460979158 6.448136e-01
[29,] 0.014277403 0.02298851 9.683314e-05 -0.885240161 3.760271e-01
[30,] 0.009622875 0.01149425 4.924586e-05 -0.266671512 7.897221e-01
[31,] 0.014258398 0.02298851 9.705244e-05 -0.886168613 3.755267e-01
[32,] 0.005453443 0.01149425 4.986245e-05 -0.855476971 3.922871e-01
[33,] 0.043283712 0.05747126 2.367109e-04 -0.922143185 3.564539e-01
[34,] 0.020763514 0.03448276 1.393165e-04 -1.162328599 2.451020e-01
[35,] 0.081261843 0.06896552 2.794398e-04 0.735582222 4.619850e-01
[36,] 0.057419907 0.05747126 2.338437e-04 -0.003358489 9.973203e-01
[37,] 0.013497133 0.02298851 9.624821e-05 -0.967459309 3.333145e-01
[38,] 0.019289310 0.03448276 1.455643e-04 -1.259299080 2.079223e-01
[39,] 0.025996272 0.04597701 1.892938e-04 -1.452256513 1.464303e-01
[40,] 0.016092694 0.03448276 1.424776e-04 -1.540671121 1.233968e-01
[41,] 0.035952614 0.05747126 2.379439e-04 -1.395011407 1.630124e-01
[42,] 0.031690963 0.05747126 2.350604e-04 -1.681505286 9.266481e-02
[43,] 0.018750079 0.03448276 1.433314e-04 -1.314110709 1.888090e-01
[44,] 0.015449080 0.02298851 9.638666e-05 -0.767944457 4.425202e-01
[45,] 0.065760689 0.06896552 2.760533e-04 -0.192889342 8.470456e-01
[46,] 0.098966900 0.05747126 2.326002e-04 2.720804542 6.512325e-03
[47,] 0.085415780 0.05747126 2.385746e-04 1.809191360 7.042128e-02
[48,] 0.038816536 0.05747126 2.343951e-04 -1.218469473 2.230456e-01
[49,] 0.038931873 0.04597701 1.893501e-04 -0.511984469 6.086619e-01
[50,] 0.055098610 0.06896552 2.760948e-04 -0.834546363 4.039732e-01
[51,] 0.033405005 0.04597701 1.916312e-04 -0.908179070 3.637836e-01
[52,] 0.043040784 0.06896552 2.829941e-04 -1.541081516 1.232969e-01
[53,] 0.011297699 0.02298851 9.615920e-05 -1.192199867 2.331829e-01
[54,] 0.040968457 0.05747126 2.356318e-04 -1.075080164 2.823388e-01
[55,] 0.023629663 0.04597701 1.877170e-04 -1.631075961 1.028743e-01
[56,] 0.006281129 0.01149425 4.916619e-05 -0.743472246 4.571958e-01
[57,] 0.063918654 0.05747126 2.369553e-04 0.418842387 6.753313e-01
[58,] 0.070325003 0.05747126 2.381374e-04 0.832943753 4.048765e-01
[59,] 0.025947288 0.03448276 1.444058e-04 -0.710289083 4.775249e-01
[60,] 0.039752578 0.04597701 1.915656e-04 -0.449718820 6.529132e-01
[61,] 0.049934283 0.05747126 2.334965e-04 -0.493238743 6.218439e-01
[62,] 0.030964195 0.04597701 1.920248e-04 -1.083386776 2.786368e-01
[63,] 0.058129184 0.05747126 2.343319e-04 0.042979051 9.657182e-01
[64,] 0.046096514 0.04597701 1.932637e-04 0.008596093 9.931414e-01
[65,] 0.012459080 0.01149425 5.008051e-05 0.136337469 8.915545e-01
[66,] 0.091447733 0.05747126 2.377744e-04 2.203411744 2.756574e-02
[67,] 0.049575872 0.02298851 9.766513e-05 2.690329952 7.138140e-03
[68,] 0.107907212 0.04597701 1.933581e-04 4.453703219 8.440175e-06
[69,] 0.019616151 0.02298851 9.789454e-05 -0.340842743 7.332220e-01
[70,] 0.032923393 0.03448276 1.454032e-04 -0.129318589 8.971056e-01
[71,] 0.030317663 0.02298851 9.867859e-05 0.737806634 4.606320e-01
[72,] 0.019437582 0.03448276 1.455870e-04 -1.246912658 2.124295e-01
[73,] 0.055245460 0.04597701 1.932838e-04 0.666667559 5.049845e-01
[74,] 0.074278054 0.05747126 2.383538e-04 1.088613505 2.763244e-01
[75,] 0.013269580 0.02298851 9.719982e-05 -0.985792573 3.242349e-01
[76,] 0.049407829 0.03448276 1.463785e-04 1.233609606 2.173484e-01
[77,] 0.028605749 0.03448276 1.455139e-04 -0.487196415 6.261191e-01
[78,] 0.039087662 0.02298851 9.801040e-05 1.626174042 1.039126e-01
[79,] 0.031447120 0.04597701 1.877464e-04 -1.060416797 2.889550e-01
[80,] 0.064005294 0.05747126 2.359641e-04 0.425361422 6.705732e-01
[81,] 0.044606529 0.05747126 2.357330e-04 -0.837897118 4.020885e-01
[82,] 0.063700493 0.06896552 2.801427e-04 -0.314565243 7.530918e-01
[83,] 0.051142205 0.04597701 1.933560e-04 0.371456331 7.102977e-01
[84,] 0.102121112 0.04597701 1.610278e-04 4.424392623 9.671399e-06
[85,] 0.021901462 0.02298851 9.843172e-05 -0.109566928 9.127528e-01
[86,] 0.064931813 0.04597701 1.929430e-04 1.364597995 1.723794e-01
[87,] 0.031747344 0.04597701 1.909867e-04 -1.029658605 3.031703e-01
[88,] 0.015893319 0.02298851 9.765131e-05 -0.718000620 4.727569e-01
attr(,"cluster")
[1] Low Low High High High High High High High Low Low High Low Low Low
[16] High High High High Low High High Low Low High Low Low Low Low Low
[31] Low Low Low High Low Low Low Low Low Low High Low Low Low Low
[46] High High Low Low Low Low High Low Low Low Low Low High Low Low
[61] Low Low Low High High High Low High Low Low High Low High High Low
[76] High Low Low Low Low Low Low High High Low High Low Low
Levels: Low High
attr(,"gstari")
[1] FALSE
attr(,"call")
localG(x = hunan$GDPPC, listw = wm62_lw)
attr(,"class")
[1] "localG"The Gi values are then joined to their corresponding hunan sf dataframe. The output vector, gi.fixed, is converted into into an r matrix object using as.matrix() (under base package). Then, cbind() (under base package) is used to join hunan sf dataframe and gi.fixed matrix to produce a new SpatialPolygonDataFrame, hunan.gi_fixed. Lastly, the field name of gi value is renamed to gstat_fixed using rename() (under dplyr package).
hunan.gi_fixed = cbind(hunan, as.matrix(gi.fixed)) %>%
rename(gstat_fixed = as.matrix.gi.fixed.)The Gi values derived using fixed distance weight matrix are then plotted side by side with the GDPPC values in hunan using the tmap package.
Question: What statistical observation can be drawn from the Gi map below?
Answer: The positive Gi values for the northeast region indicate High-High clustering, while the negative Gi values for the northwest and central-west regions indicate Low-Low clustering.
gdppc = qtm(hunan, "GDPPC")
Gimap_fixed = tm_shape(hunan.gi_fixed) +
tm_fill(col = "gstat_fixed",
style = "pretty",
palette="-RdBu",
title = "local Gi") +
tm_borders(alpha = 0.5)
tmap_arrange(gdppc, Gimap_fixed, asp=1, ncol=2)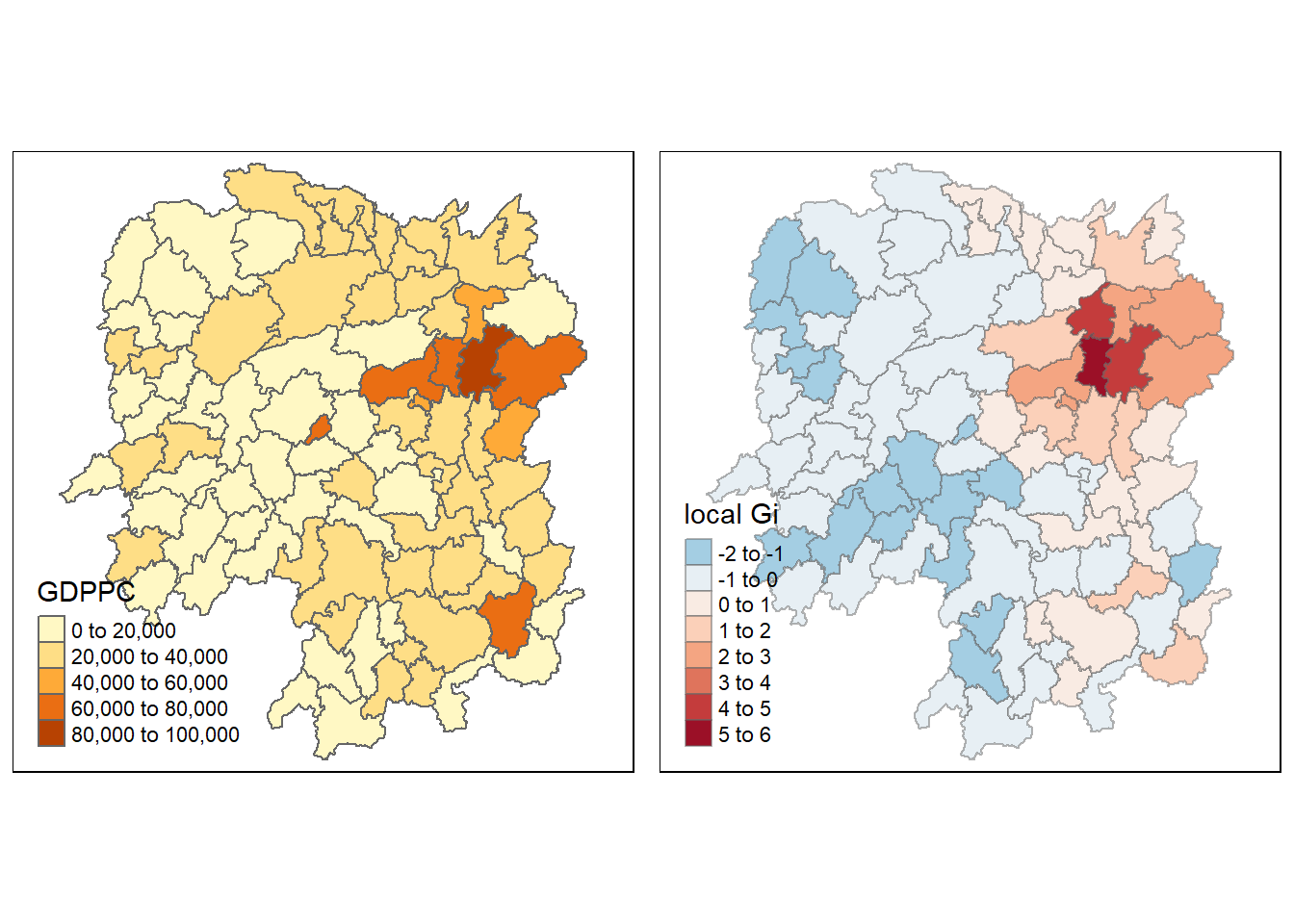
Student Note:
Gi values indicate the local intensity of spatial clustering for each county for GDPPC.
Positive Gi values mean High-High clustering.
Negative Gi mean Low-Low clustering.
Values around zero indicate no significant spatial clustering.
Z-scores represent how many standard deviations an observed Gi value is from the mean Gi value.
Positive Z-scores indicate that the observed Gi is higher than the average, suggesting significant clustering.
Negative Z-scores indicate that the observed Gi is lower than the average, suggesting significant dispersion.
Significance (Pr(z != E(Gi))) represent the p-values associated with each Gi value, which indicate the statistical significance of the local clustering. Small p-values (typically below 0.05) suggest that the observed clustering or dispersion is unlikely to have occurred by random chance.
Cluster Identification (attr(,“cluster”)) categorises each observation as either “Low” or “High” based on the local spatial autocorrelation pattern.
“Low” indicates observations that are part of a Low-Low or High-High cluster.
“High” indicates observations that are part of a High-Low or Low-High cluster.
Attribute Information (attr(,“gstari”)) is set to FALSE, indicating that the analysis was not run under a global model.
- If set to TRUE, it would mean that the observation contributes to the global spatial autocorrelation.
10.9.2 Gi Statistics Using Adaptive Distance and Mapping Gi Values with Adaptive Distance Weights
The Gi values for GDPPC 2012 is computed using adaptive distance weights, knn_lw.
The Gi values are then joined to their corresponding hunan sf dataframe. The output vector, gi.adaptive, is converted into into an r matrix object using as.matrix() (under base package). Then, cbind() (under base package) is used to join hunan sf dataframe and gi.adaptive matrix to produce a new SpatialPolygonDataFrame, hunan.gi_adaptive. Lastly, the field name of gi value is renamed to gstat_fixed using rename() (under dplyr package).
fips = order(hunan$County)
gi.adaptive = localG(hunan$GDPPC, knn_lw)
hunan.gi_adaptive = cbind(hunan, as.matrix(gi.adaptive)) %>%
rename(gstat_adaptive = as.matrix.gi.adaptive.)The Gi values derived using adaptive distance weight matrix are then plotted side by side with the GDPPC values in hunan using the tmap package.
Question: What statistical observation can be drawn from the Gi map below?
Answer: The Gi values show a more graduated change from the northeast region to the central-west region, from positive to negative values. However, similar to fixed distance weights, the adaptive distance weights output also indicates High-High clustering in the northeast, and Low-Low clustering in the central-west.
gdppc = qtm(hunan, "GDPPC")
Gimap_adaptive = tm_shape(hunan.gi_adaptive) +
tm_fill(col = "gstat_adaptive",
style = "pretty",
palette="-RdBu",
title = "local Gi") +
tm_borders(alpha = 0.5)
tmap_arrange(gdppc,
Gimap_adaptive,
asp=1,
ncol=2)
Student Note: On choosing between fixed distance weights and adaptive distance weights for GDPPC across counties in Hunan province, the latter may be more appropriate given that GDPPC appears to be more concentrated in the northeast region, which includes the provincial capital, Changsha, and the surrounding counties. Also, it is unlikely that the spatial processes influencing GDPPC are uniform across the entire study area since local development is affected by more than just distance from the provincial capital. Factors such as physical landscape (mountains, rivers), transport networks as well as socioeconomic policies (e.g., education, tourism) are not evenly developed throughout a province. Hence, an adaptive distance weights approach reflects the varying influence of different factors across space, and allows the analysis to capture the nuanced geospatial processes affecting GDPPC.
~~~ End of Hands-on Exercise 2B ~~~